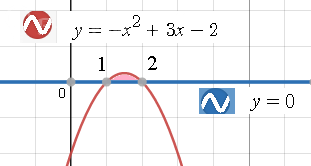
Задача 65188 найдите площадь фигуры ограниченной...

Андрей_365047160

22 июня 2022 г. в 06:37

найдите площадь фигуры ограниченной линиями y=–x²+3x–2; y=0

exponenta

22 июня 2022 г. в 09:04

★

–x²+3x–2=0
x²–3x+2=0
D=(–3)²–4·2=1
x₁=(3–1)/2; x₂=(3+1)/2
x₁=1; x₂=2


S= ∫ ₁²(–x²+3x–2)dx= (–(x³/3)+3·(x²/2)–2x)| ₁²=–(2³/3)+3·(2²/2)–2·2)+(1³/3)–3·(1²/2)+2·1=...