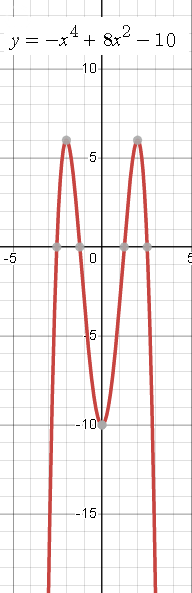
Задача 65011 Исследовать функцию с помощью...
Условие
Решение
1) D(y)=(–∞;+ ∞)
Вертикальных асимптот нет
2) Функция является чётной
у(-х)=-(-x)^4+8*(-x)^2-10=-x^4+8x^2-10
y(-x) = y(x)
3)lim_(x→ +∞ ))f(x)=-∞
lim_(x→-∞ )f(x)=-∞
Горизонтальных асимптот нет
Наклонной асимптоты нет, так как
k=lim_(x→∞ )(-x^4+8x^2-10/x=∞
Исследование с помощью первой производной
y`=(-x^4+8x^2-10)`
y`=-4x^3+16x;
y`=0
-4x^3+16x=0
-4x(x^2-4)=0
x=0; x= ± 2
Знак производной
___+___ (-2) __-__ (0) ___+__ (2) __-__
x=0 – точка минимума, производная меняет знак с - на +
x= ± 2 - точки максимума, производная меняет знак с + на -
y`>0 при x∈ (- ∞ ;-2) и (0;2)
Функция возрастает при x∈ x∈ (- ∞ ;-2) и (0;2)
y`<0 при x∈ (- 2;0 )и при х ∈ (2;+ ∞)
Функция убывает при x∈ (- 2;0 )и при х ∈ (2;+ ∞)
Исследование с помощью второй производной
y``=(-4x^3+16x)`=-12x^2+16
y`` =0
-12x^2+16=0
x^2=4/3
x= ± 2sqrt(3)/3 - точки перегиба
___+__ (-2sqrt(3)/3) ____-____ (2sqrt(3)/3) ___+__
y`` > 0 ⇒ функция выпукла вниз ( ∪) на (- ∞ ;(-2sqrt(3)/3) ) и на ((2sqrt(3)/3) ;+ ∞ )
y`` < 0 ⇒ функция выпукла вверх ( ∩) на (-(-2sqrt(3)/3) ;(2sqrt(3)/3) )