Задача 65008 Решить систему уравнений и найти частные...
Условие
удовлетворяют приведенным начальным условиям.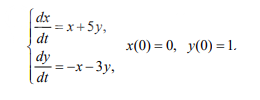
Решение
x`(t)=x+5y\\y`(t)=-x-3y \end{matrix}\right.[/m]
Выразим из второго уравнения [m]x[/m] и подставим в первое уравнение:
[m]\left\{\begin{matrix}
(-y`-3y)`=-y`-3y+5y\\x=-y`-3y\end{matrix}\right.[/m]
Решаем первое уравнение:
[m]-y``-3y`=-y`+2y [/m]
[m]y``+2y`+2y=0[/m]
получили линейное [i]однородное дифференциальное уравнение второго порядка с постоянными коэффициентами[/i]
Cоставляем характеристическое уравнение:
[m]k^2+2k+2=0[/m]
D=2^2-4*2=4-8=-4
[m]k_{1}=-1-i[/m] и [m]k_{2}=-1+i[/m] - корни комплексно-сопряженные
α =-1
β =1
Общее решение однородного уравнения в таком случае имеет вид:
y_(общее однород)=[m]e^{-t}\cdot (C_{1}cost +C_{2}sint)[/m]
Находим
y`_(общее однород)=[m]e^{-t}\cdot (-t)`\cdot (C_{1}cost +C_{2}sint)+e^{-t}\cdot (C_{1}\cdot (cost)` +C_{2}\cdot (sint)`)[/m]
y`_(общее однород)=[m]-e^{-t}\cdot (C_{1}cost +C_{2}sint)+ e^{-t}\cdot (C_{1}\cdot (-sint)+C_{2}\cdot (cost)[/m]
y`_(общее однород)=[m]e^{-t}\cdot (C_{1}(-cost-sint) +C_{2}(cost-sint))[/m]
Подставляем
y_(общее однород)=[m]e^{-t}\cdot (C_{1}cost +C_{2}sint)[/m]
и
y`_(общее однород)=[m]e^{-t}\cdot (C_{1}(-cost-sint) +C_{2}(cost-sint))[/m]
во второе уравнение [m]x=-y`-3y[/m]
получаем:
x_(общее однород)=[m]e^{-t}\cdot (C_{1}(cost-sint) +C_{2}(sint+cost))-3\cdot e^{-t}\cdot (C_{1}cost +C_{2}sint)[/m]
x_(общее однород)=[m]e^{-t}\cdot (C_{1}(-4cost-sint)+C_{2}\cdot (cost-4sint))[/m]
Итак, общее решение системы:
[m]\left\{\begin{matrix}
y(t)=e^{-t}\cdot (C_{1}cost +C_{2}sint)\\x(t)=e^{-t}\cdot (C_{1}(-4cost-sint)+C_{2}\cdot (cost-4sint))\end{matrix}\right.[/m]
Начальные условия
x(0)=0
y(0)=1
[m]\left\{\begin{matrix}
y(0)=e^{0}\cdot (C_{1}cos0 +C_{2}sin0)\\x(0)=e^{0}\cdot (C_{1}(-4cos0-sin0)+C_{2}\cdot (cos0-4sin0))\end{matrix}\right.[/m] ⇒
[m]\left\{\begin{matrix}
1=e^{0}\cdot (C_{1}cos0 +C_{2}sin0)\\0=e^{0}\cdot (C_{1}(-4cos0-sin0)+C_{2}\cdot (cos0-4sin0))\end{matrix}\right.[/m] ⇒
Решаете систему и находите:
C_(1)=
C_(2)=
