Задача 64868 Исследовать на непрерывность функции,...
Условие
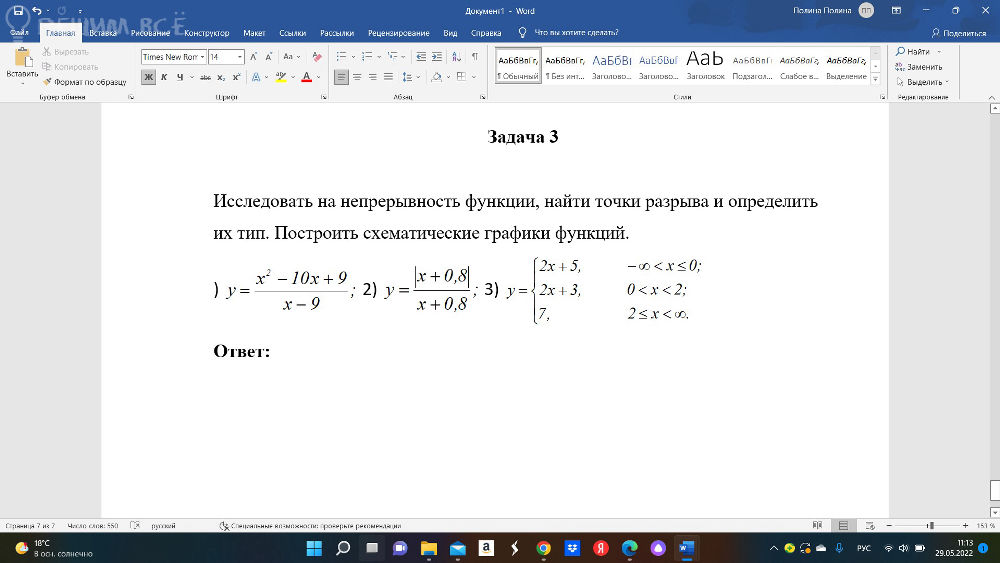
Исследовать на непрерывность функции, найти точки разрыва и определить их тип. Построить схематические графики функций.
Решение
Область определения x-9≠ 0
Функция непрерывна во всех точках, кроме х=9 как частное непрерывных функций
x^2-10x+9=(x-1)(x-9)
[m]\frac{x^2-10x+9}{x-9}=x-1[/m] при x ≠ 9
Находим предел слева,
lim_(x →9-0)f(x)=lim_(x →9 -0)(x-1)=8
Находим предел справа,
lim_(x →9+0)f(x)=lim_(x →9 +0)(x-1)=8
Предел слева равен пределу справа.
Функция имеет предел в точке, но не определена в этой точке
Значит,
x=9 - точка устранимого разрыва.
2)
Область определения x+0,8≠ 0
Функция непрерывна во всех точках, кроме х=-0,8
Находим предел слева, т.е.
при х+0,8 < 0
|x+0,8|=-(x+0,8)
Тогда
[m]y=\frac{-(x+0,8)}{x+0,8}[/m]
при x ≠ - 0,8
[m]y=-1[/m] при х < -0,8
lim_(x →-0,8-0)f(x)=lim_(x →-2 -0)(-1)=-1
Находим предел справа
при х+0,8 ≥ 0
|x+0,8|=x+0,8
Тогда
[m]y=\frac{x+0,8}{x+0,8}[/m]
при x ≠ - 0,8
[m]y=1[/m] при x >- 0,8
lim_(x →-0,8 +0)f(x)=lim_(x →-0,8 +0)(1)=1
предел слева ≠ пределу справа
Функция имеет скачок ([i]конечный[/i]) в точке x=-0,8
х=-0,8 - [i]точка разрыва первого рода[/i]
3)
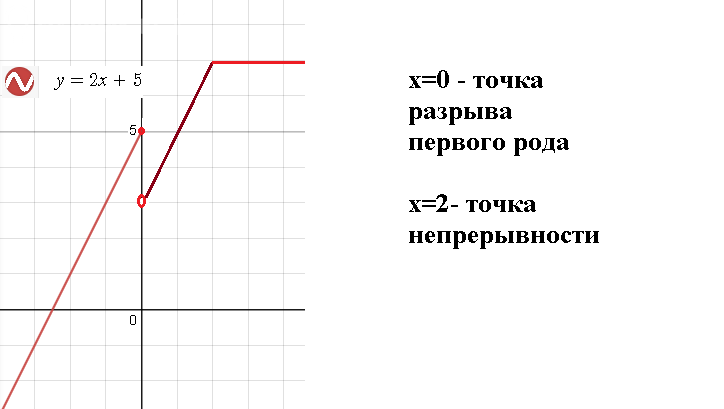
На (-∞ ;0] функция непрерывна, так как y=2х+5 непрерывна на (- ∞ ;+ ∞ )
На (0;2) функция непрерывна, так как y=2x+3 непрерывна на (- ∞ ;+ ∞ )
На [2;+∞) функция непрерывна, так как y=7 непрерывна на (- ∞ ;+ ∞ )
Значит, надо выяснить непрерывность функции в точках
х=0 и х=2
Исследуем точку х=0
Находим предел слева:
lim_(x →-0)f(x)=lim_(x → -0)(2х+5)=0+5=5
Находим предел справа:
lim_(x → +0)f(x)=lim_(x → +0)(2x+3)=0+3=3
предел слева ≠ пределу справа
Функция имеет скачок ([i]конечный[/i]) в точке x=0
х=0 - [i]точка разрыва первого рода[/i]
Исследуем точку х=2
Находим предел слева:
lim_(x →2-0)f(x)=lim_(x →2 -0)(2х+3)=2*2+3=7
Находим предел справа:
lim_(x →2 +0)f(x)=lim_(x →2 +0)7=7
f(2)=7
Предел слева равен пределу справа, равен значению функции в точке
х=2 - точка непрерывности