Задача 646 Найдите наименьшее значение функции y =...

slava191

21.02.2014

Найдите наименьшее значение функции y = (x + 6)^2(x + 3) + 11 на отрезке [-5; 5]

Находим производную функции
y' = 2(x + 6)(x + 3) + (x + 6)2
y' = (x + 6)(2x + 6 + x + 6)
y' = (x + 6)(3x + 12)
y' = 3(x + 6)(x + 4)
Находим нули производной y'=0
Расставляем промежутки знакопостоянства и находи Ymin=y(X min)
y(-4) = (-4 + 6)2(-4 + 3) + 11 = -4 + 11 = 7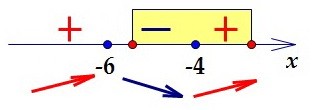

Ответ: 7