Задача 64548 Вычислить объем тела...
Условие
оси Оy трапеции, образованной
прямыми y = 3x, у = 2, у=4 и осью
ординат.
математика колледж
1643
Решение
★
считайте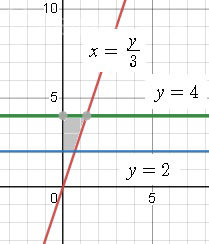
оси Оy трапеции, образованной
прямыми y = 3x, у = 2, у=4 и осью
ординат.
считайте