Задача 64518 вдоль прямой дороги находятся дома A, B,...
Условие
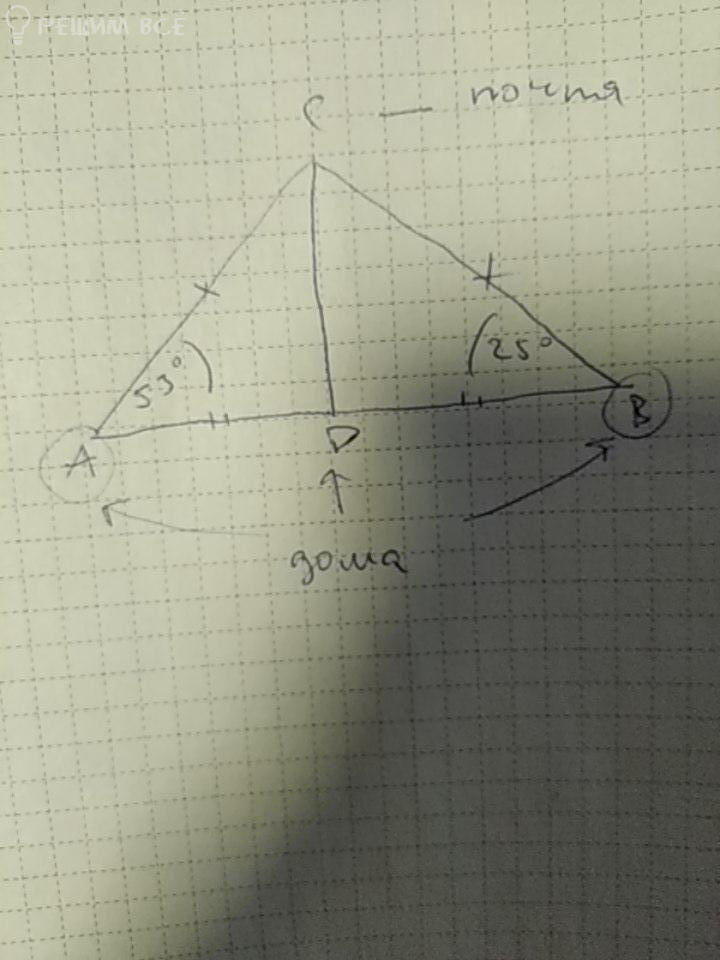
Решение
AD=BD=(1860/2)м= 930 м
D- середина AB ⇒ [b]CD - медиана[/b] треугольника АВС
∠ АСВ=180 ° - ∠ CAB - ∠ АВС =180 ° -53°-25°=102 °
По теореме синусов:
[m] \frac{AB}{sin∠ АСВ}=\frac{AC}{sin ∠АВС}=\frac{BC}{sin ∠СAB }[/m]
[m] \frac{1860}{sin 102 ° }=\frac{AC}{sin 25 ° }=\frac{BC}{sin 53 ° }[/m] ⇒
[m] \frac{1860}{sin 102 ° }=\frac{AC}{sin 25 ° }[/m] найдем АС
[m] \frac{1860}{sin 102 ° }=\frac{BC}{sin 53 ° }[/m] найдем ВС
Из треугольника АСD по теореме косинусов
CD^2=AC^2+AD^2-2AC*AD*cos ∠ ∠ CAB=
Сравиваем
AD+CD=
с
AC
Аналогично
BD+CD
c
BC