Задача 64412 решить неравенство Тв„( 22 юв„ Х < ов( -...
Условие
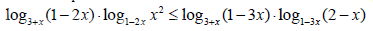
Решение
[m]\left\{\begin {matrix}1-2x>0\\3+x>0\\3+x ≠1\\2-x>0\\x^2>0\\1-3x>0\\1-3x ≠ 1 \end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x<\frac{1}{2}\\x>-3\\x ≠-2\\x<2\\x ≠ 0\\x<\frac{1}{3}\\x ≠ 0 \end {matrix}\right.[/m] ⇒
[m]x ∈ (-3; -2)\cup(-2;0)\cup(0;\frac{1}{3})[/m]
В условиях ОДЗ переход к другому основанию и применение свойств логарифмов:
[m]\frac{lg(1-2x)}{lg(3+x)} \cdot \frac{lgx^2}{lg(1-2x)} ≤ \frac{lg(1-3x)}{lg(3+x)}\cdot \frac{lg(2-x)}{lg(1-3x)}[/m]
Так как
x ≠ 0 ⇔ [m]lg(1-2x) ≠ 0[/m] и [m]lg(1-3x) ≠ 0[/m]
сокращаем и получаем неравенство:
[m]\frac{lgx^2}{lg(3+x)} ≤ \frac{lg(2-x)}{lg(3+x)}[/m]
1) Если x ∈ (-3; -2), то 3 + x ∈ (0; 1), тогда lg(3+x) < 0
Умножаем неравенство на lg(3+x), при этом меняется знак:
lg(x^2) >= lg(2-x)
Так как функция y = lg(x) строго возрастает, можно просто избавиться от логарифмов:
x^2 >= 2 - x
x^2 + x - 2 >= 0
(x + 2)(x - 1) >= 0
x ∈ (-oo; -2] U [1; +oo)
Но по ОДЗ x ∈ (-3; -2), поэтому:
x1 ∈ (-3; -2)
2) Если x ∈ (-2; 0) U (0; 1/3), то 3 + x > 1, тогда lg(3+x) > 0
Умножаем неравенство на lg(3+x), при этом знак остается:
lg(x^2) <= lg(2-x)
Так как функция y = lg(x) строго возрастает, можно просто избавиться от логарифмов:
x^2 <= 2 - x
x^2 + x - 2 <= 0
(x + 2)(x - 1) <= 0
x ∈ [-2; 1]
Но по ОДЗ x ∈ (-2; 0) U (0; 1/3), поэтому:
x2 ∈ (-2; 0) U (0; 1/3)
Забавно получилось: решение неравенства - это более широкие промежутки, чем ОДЗ, поэтому окончательный ответ равен ОДЗ.
[b]Ответ[/b]: x ∈ (-3; -2) U (-2; 0) U (0; 1/3)
Все решения
Мы остановились на том, что ОДЗ: x ∈ (-3; -2) U (-2; 0) U (0; 1/3)
И неравенство:
[m]\frac{lg(x^2)}{lg(3+x)} <= \frac{lg(2-x)}{lg(3+x)}[/m]
1) Если x ∈ (-3; -2), то 3 + x ∈ (0; 1), тогда lg(3+x) < 0
Умножаем неравенство на lg(3+x), при этом меняется знак:
lg(x^2) >= lg(2-x)
Так как функция y = lg(x) строго возрастает, можно просто избавиться от логарифмов:
x^2 >= 2 - x
x^2 + x - 2 >= 0
(x + 2)(x - 1) >= 0
x ∈ (-oo; -2] U [1; +oo)
Но по ОДЗ x ∈ (-3; -2), поэтому:
x1 ∈ (-3; -2)
2) Если x ∈ (-2; 0) U (0; 1/3), то 3 + x > 1, тогда lg(3+x) > 0
Умножаем неравенство на lg(3+x), при этом знак остается:
lg(x^2) <= lg(2-x)
Так как функция y = lg(x) строго возрастает, можно просто избавиться от логарифмов:
x^2 <= 2 - x
x^2 + x - 2 <= 0
(x + 2)(x - 1) <= 0
x ∈ [-2; 1]
Но по ОДЗ x ∈ (-2; 0) U (0; 1/3), поэтому:
x2 ∈ (-2; 0) U (0; 1/3)
Забавно получилось: решение неравенства - это более широкие промежутки, чем ОДЗ, поэтому окончательный ответ равен ОДЗ.
Ответ: x ∈ (-3; -2) U (-2; 0) U (0; 1/3)