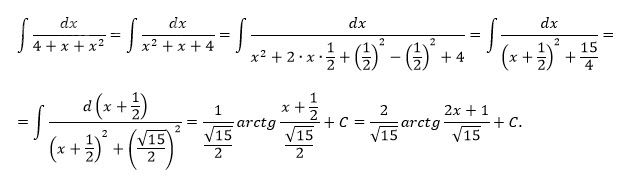Задача 63717 1. Интегрирование рациональных функций...
Условие
математика колледж
241
Решение
★
[m]x^2+x+4=(x+\frac{1}{2})^2+\frac{15}{4}[/m]
Замена
[m]x+\frac{1}{2}=t[/m]
[m]dx=dt[/m]
табличный интеграл ( cм. скрин)
[m]a^2=\frac{15}{4}[/m]
[m] ∫\frac{dt}{t^2+\frac{15}{4}}= \frac{1}{\frac{\sqrt{15}}{2}} arctg \frac{t}{\frac{\sqrt{15}}{2}}+C[/m]
[m]t=x+\frac{1}{2}[/m]
[m] ∫\frac{dx}{x^2+x+4}= \frac{2}{\sqrt{15}} arctg \frac{2x+1}{\sqrt{15}}+C[/m]
О т в е т. [m] ∫\frac{dx}{x^2+x+4}= \frac{2}{\sqrt{15}} arctg \frac{2x+1}{\sqrt{15}}+C[/m]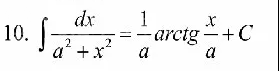
Все решения
