Задача 63701 ...
Условие
y=x^2-4x+3, y=0, x=3 и x=4
《Интегралы и его применение》
математика колледж
528
Решение
★
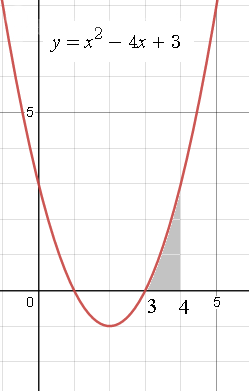
y=x^2-4x+3, y=0, x=3 и x=4
《Интегралы и его применение》
