Задача 63693 Вам предложена функция. проведите...
Условие
2. Найти точки пересечения с осями.
3. Исследовать функцию на четность/нечетность.
4. Найти асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти дополнительные точки, уточняющие график.
8. Построить график.
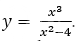
Решение
Область определения (- ∞ ;-2) U (-2;2) U(2;+ ∞ )
2.Точки пересечения с осями.
3. Исследовать функцию на четность/нечетность.
4. Найти асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
Находим производную
Применяем правило дифференцирования частного ( дроби):
(u/v)`=(u`*v-u*v`)/v^2
y`= ((x^3)`*(x^2-4)-x^3*(x^2-4)`)/(x^2-4)^2
y`=((3x^2*(x^2-4)-x^3*(2x))/(x^2-4)^2
y`=(x^4 -12x^2)/(x^2-4)^2
y`=0
x^4 - 12x^2=0
x^2*(x^2-12)=0 ⇒
x^2 = 0 или x^2=12
x=0 или х = ± 2sqrt(3)
Знак производной:
__+___ (-2sqrt(3)) _-_ (-2) __-__ (0) _-__ (2) __-__ (2sqrt(3)) __+__
y`<0 на (-2sqrt(3); - 2) и на (-2; 2 ) и на (2; 2sqrt(3)) , значит функция монотонно убывает на (-2sqrt(3); - 2) и на (-2; 2 ) и на (2; 2sqrt(3))
y`>0 на (- ∞ ;-2sqrt(3)) и на (2sqrt(3);+ ∞ ) , значит функция монотонно возрастает на (- ∞ ;-2sqrt(3)) и на (2sqrt(3);+ ∞ )
x=-2sqrt(3) - точка максимума
f(-2sqrt(3))=(-2sqrt(3))^2/((-2sqrt(3))^2-4)= -3sqrt(3)
х=2sqrt(3) - точка минимума
f(2sqrt(3))=(2sqrt(3))^2/((2sqrt(3))^2-4)= 3sqrt(3)
6. Найти интервалы выпуклости функции и точки перегиба.
Находим вторую производную
y``=((x^4 -12x^2)/(x^2-4)^2)`
Применяем правило дифференцирования частного ( дроби):
(u/v)`=(u`*v-u*v`)/v^2
u=x^4-12x^2
v=(x^2-4)^2
u`=4x^3-24x
v`=2*(x^2-4)*(x^2-4)`=2*(x^2-4)*(2x)=4x(x^2-4)
y``=((4x^3-24x)*(x^2-4)^2-(x^4-12x^2)*4x*(x^2-4))/(x^2-4)^4
y``=((4x^3-24x)*(x^2-4)-(x^4-12x^2)*4x)/(x^2-4)^3
y``=(8x^3+96x)/(x^2-4)^3
y``=8x(x^2+12)/(x^2-4)^3
___________-______ (-2) ____+_____ (0) ____-____ (2) ______+____
y``<0 на (- ∞ ;-2) и на (0;2)
кривая выпукла вверх на (- ∞ ;-2) и на (0;2)
y``>0 на (-2 ;0) и на (2;+ ∞ )
кривая выпукла вниз на (-2 ;0) и на (2;+ ∞ )
7. Найти дополнительные точки, уточняющие график.
Находите самостоятельно.
x=1 ⇒ y=1^3/(1^2-4)=
x=3 ⇒ y=3^3/(3^2-4)=
8. Построить график.