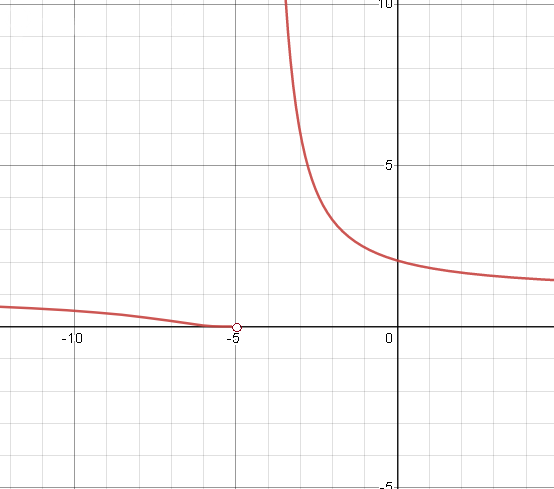
Задача 63513 Задача 1. Исследовать на непрерывность...

ifdyuvx687

4 марта 2022 г. в 17:21

Задача 1. Исследовать на непрерывность функцию и построить ее схему.

exponenta

5 марта 2022 г. в 11:14

★

Функция не определена в точке x=–5

Так как (х+5) – знаменатель дроби (2/(х+5))


В остальных точках функция непрерывна, как композиция непрерывных функция

u= (2/(х+5))

и

6^u – показательная функция, непрерывна при всех u


Находим односторонние пределы:

Предел слева в точке x=–5

lim_{x→–5 –0} f(x)=6^{lim_{x→–5 –0}2/(x+5)}=6^–∞=0

Предел
lim_{x→ –5+0} f(x)=2^{lim_{x→–5 +0}2/(x+5)}=2^+∞=+∞

Правосторонний предел равен +∞ ,

значит х=–5 – точка разрыва второго рода.