Задача 63321 Найти точки разрыва функции, если они...
Условие
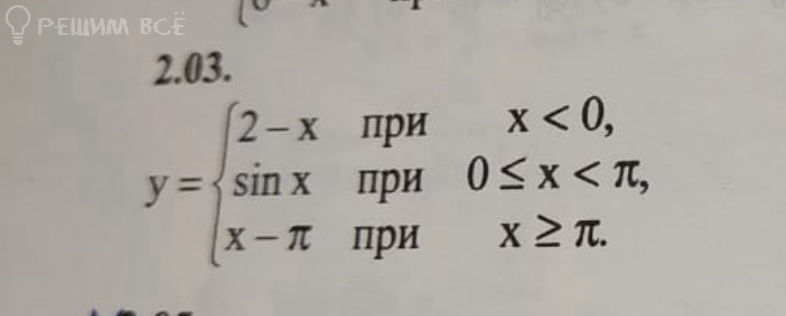
Решение
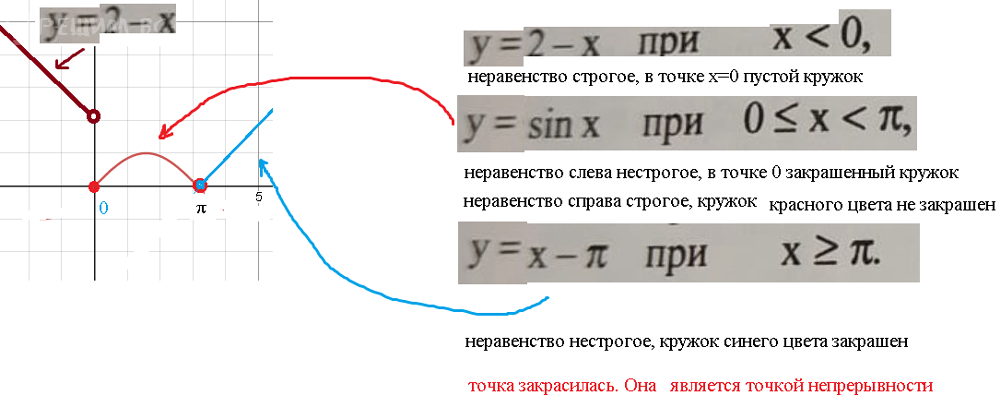
На (0;π) функция непрерывна, так как y=sinx непрерывна на (- ∞ ;+ ∞ )
На (π;+ ∞ ) функция непрерывна, так как y=x-π непрерывна на (- ∞ ;+ ∞ )
Значит, надо выяснить непрерывность функции в точках
х=0 и х=π
x=0
Находим предел слева:
lim_(x → -0)f(x)=lim_(x → -0)(2-x=2-(-0)=2
Находим предел справа:
lim_(x → +0)f(x)=lim_(x →- +0)(sinx)=sin(+0)=0
предел слева ≠ пределу справа Это означает, что функция не имеет предела в точке
Значит[b] не является [/b][i]непрерывной[/i]
Функция имеет скачок ([i]конечный[/i]) в точке x=0
который равен разности значений справа и слева
Справа y(0)=sin0=0
Cлева y(0)=2-0=2
Скачок 0-(-2)=2 - скачок ([i]конечный[/i])
х=0 - [i]точка разрыва первого рода[/i]
x=π
Находим предел слева:
lim_(x →π -0)f(x)=lim_(x →π-0)sinx=sin(π -0)=0
Находим предел справа:
lim_(x →π +0)f(x)=lim_(x →π+0)(x-π)=(π +0)-π=0
предел слева = пределу справа lim_(x →π -0)f(x)=lim_(x →π +0)f(x)
Это означает, что функция имеет предел в точке
lim_(x →π )f(x)=[b]0[/b]
По определению непрерывности этот предел должен равняться значению функции в точке
f(π)=sinπ=[b]0[/b]
Так как lim_(x →π )f(x)=f(π),
то значит, функция непрерывна в точке х=π
x=π - точка [i]непрерывности[/i]