Задача 63309 Задание под номером 3 Исследование...

Guf

18 февраля 2022 г. в 06:42

Задание под номером 3

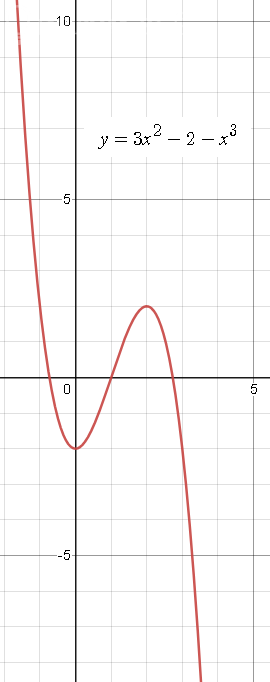
Исследование функции:

exponenta

18 февраля 2022 г. в 11:42

★

Область определения (– ∞ ;+ ∞ )

y`=(3x<sup>2</sup>–2–x<sup>3</sup>)`=6x–3x²

y`=0

6x–3x²=0

3x·(2–x)=0

x=0 или х=2

Расставляем знак производной

Например, так : y`(10) =6·10–3·10²<0

Cправа от 2 ставим минус и
далее чередуем справа налево:

__–__ (0) _+___ (2) ___–__

б)

х=2 – точка максимума, производная меняет знак с + на –
х=0 – точка минимума, производная меняет знак с – на +

а)
y`< 0 на (– ∞ ;0) и на (2;+ ∞ )
Функция убывает на на (– ∞ ;0) и на (2;+ ∞ )

y`>0 на (0;2)
Функция возрастает на на (0;2)