Задача 62885 ...
Условие
математика
1091
Решение
★
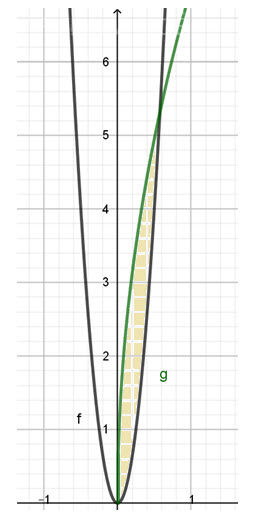
256x^4=49x
x*(256x^3-49)=0
x=0 или x=[m]\sqrt[3]\frac{49}{256}[/m]
[m]S= ∫_{0} ^{\sqrt[3]\frac{49}{256}}(7\sqrt{x}-16x^2)dx=(7\cdot \frac{x^{\frac{3}{2}}}{\frac{3}{2}}-16\frac{x^3}{3})|_{0} ^{\sqrt[3]\frac{49}{256}}=[/m]
[m]x=\sqrt[3]\frac{49}{256}[/m] ⇒ [m]x^3=\frac{49}{256}[/m] ⇒ [m]\sqrt{x^3}=\sqrt{\frac{49}{256}}=\frac{7}{16}[/m]
[m]=(7\cdot \frac{2}{3}\cdot \sqrt{x^3}-\frac{16}{3}\cdot x^3)|_{0} ^{\sqrt[3]\frac{49}{256}}=[/m]
[m]=7\cdot \frac{2}{3}\cdot \sqrt{\frac{49}{256}}-\frac{16}{3}\cdot\frac{49}{256}=7\cdot \frac{2}{3}\cdot \frac{7}{16}-\frac{49}{3\cdot 16}=\frac{98}{48}-\frac{49}{48}=\frac{49}{48} [/m]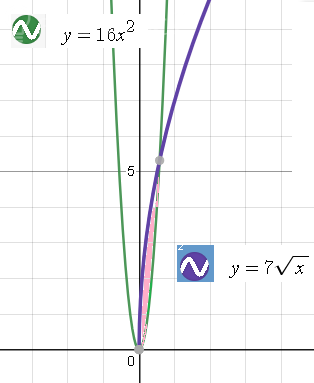
Все решения