Задача 62712 Провести полное исследование всех...
Условие

Решение
Функция не является ни чётной, ни нечётной, ни периодической
Область определения симметрична относительно 0
но
[m] y(-x)=\frac{ 1-2(-x)^3}{(-x)^2}=\frac{1+2 x^3}{x^2}[/m]
[m]y(-x) ≠ y(x)[/m] и [m]y(-x) ≠- y(x)[/m]
Прямая [m] x=0 [/m] является [i] вертикальной[/i] асимптотой.
Так как [m] lim_{x → 0}\frac{1-2 x^3}{x^2}=+ ∞ [/m]
[i]Горизонтальных[/i] асимптот нет, так как
[m] lim_{x → ∞}\frac{1-2 x^3}{x^2}= ∞ [/m]
Наклонная асимптота:
[m] k= lim_{x → ∞}\frac{f(x)}{x}=lim_{x → ∞}\frac{1-2 x^3}{x^3}= -2[/m]
[m]k=-2[/m]
[m]b= lim_{x → ∞}(\frac{1-2 x^3}{x^2}-(-2)x)= lim_{x → ∞}\frac{1-2x^3+2x^3}{x^2}= 0[/m]
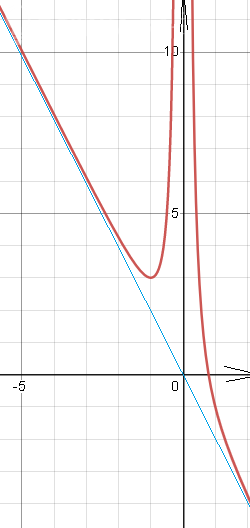
[m]y=-2x[/m] - [i] наклонная асимптота[/i].
[b]Исследование с помощью первой производной[/b]:
[m]y`=(\frac{1-2 x^3}{x^2})`[/m]
[m]y`=\frac{(1-2 x^3)`\cdot x^2-(1-2x^3)\cdot (x^2)`}{(x^2)^2}[/m]
[m]y`=\frac{(-6 x^2)`\cdot x^2-(1-2x^3)\cdot (2x)}{(x^2)^2}[/m]
[m]y`=\frac{-6x^4-2x+4x^4}{x^4}[/m]
[m]y`=\frac{-2(x^3+1)}{x^3}[/m]
y`=0
x=-1; x=0
Расставляем знак производной на ОДЗ:
____-_ (-1) ___+___ (0) ____-__
y`<0 на (- ∞ ; -1) и на (0;+ ∞ )
Значит функция убывает на (- ∞ ; -1) и на (0;+ ∞ )
y`>0 на (-1;0)
Значит, функция возрастает на (-1;0)
x=-1 - точка минимума, производная меняет знак с - на +
[m]y(-1)=\frac{1-2 \cdot (-1)^3}{(-1)^2}=3[/m]
[b]Исследование с помощью второй производной:[/b]
[m]y``=(y`)`=(\frac{-2(x^3+1)}{x^3})`=(-2-2x^(-3))`=6x^(-4)=\frac{6}{x^4}[/m]
[m]y`` >0 [/m] на (- ∞;0) и на (0;+ ∞ ) ⇒ функция выпукла вниз на на (- ∞;0) и на (0;+ ∞ )
точек перегиба нет