Задача 62590 геометрическая прогрессия. a10...
Условие
a10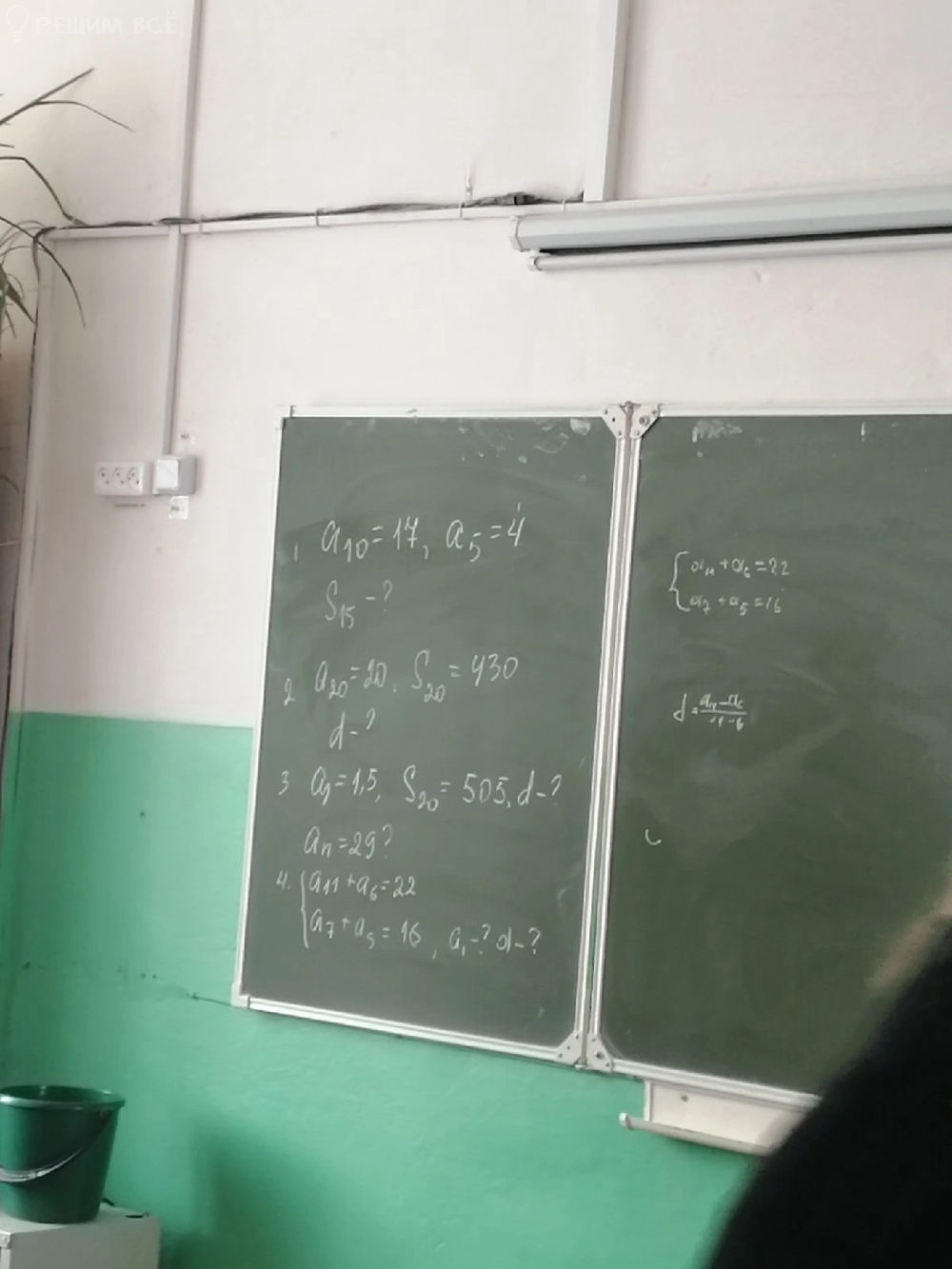
Решение
[m]a_{10}=a_{1}+d(10-1)[/m] ⇒ [m]a_{10}=a_{1}+9d[/m]
[m]a_{5}=a_{1}+d(5-1)[/m] ⇒ [m]a_{5}=a_{1}+4d[/m]
По условию
[m]a_{10}=17[/m] ⇒ [m]a_{1}+9d=17[/m]
[m]a_{5}=4[/m] ⇒ [m]a_{1}+4d=4[/m]
Получаем систему двух уравнений:
[m]\left\{\begin {matrix}a_{1}+9d=17\\a_{1}+4d=4\end {matrix}\right.[/m]
Вычитаем из первого уравнения второе:
[m]\left\{\begin {matrix}5d=13\\a_{1}+4d=4\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}d=2,6\\a_{1}+4\cdot 2,6=4\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}d=2,6\\a_{1}=-6,4\end {matrix}\right.[/m]
[m]S_{n}=\frac{2a_{1}+d(n-1)}{2}[/m]- формула [i]суммы n первых членов [/i]арифметической прогрессии
[m]S_{15}=\frac{2a_{1}+d\cdot(15-1)}{2}=\frac{2\cdot (-6,4)+2,6\cdot 14)}{2}=[/m]