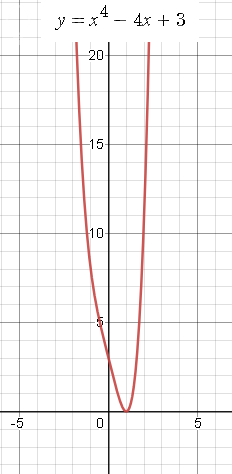
Задача 62472 Постройте график функции f(x)=x^4-4x+3...
Условие
Решение
1) D(y)=(–∞;+ ∞)
Вертикальных асимптот нет
2) Функция не является ни чётной, ни нечётной.
у(-х)=(-x)^4-4*(-x)+3=x^4+4x+3
y(-x) ≠ y(x)
3)lim_(x→ +∞ ))f(x)=+∞
lim_(x→-∞ )f(x)=+∞
Горизонтальных асимптот нет
Наклонной асимптоты нет, так как
k=lim_(x→∞ )(x^4-4x+3)/x=∞
4)
Точки пересечения с осью Ох:
f(x)=0
x^4-4x+3=0
x^4-1-4x+4=0
(x^4-1)-4(x-1)=0
(x^2-1)(x^2+1)-4(x-1)=0
(x-1)(x+1)(x^2+1)-4(x-1)=0
(x-1)*(x^3+x^2+x+1-4)=0
x=1
(1;0) -точка пересечения с осью Ох, других точек нет, так как уравнение x^3+x^2+x+1-4=0 не имеет корней
При х=0 у=3
(0;3) - точка пересечения с осью Оу.
5)
y`=(x^4-4x+3)`
y`=4x^3-4;
y`=0
x^3-1=0
x=1
Знак производной
___-___ (1) __+__
x=1 –минимума, производная меняет знак с - на +
x
y`>0 при x∈ (1;+ ∞)
Функция возрастает при x∈ (1;+ ∞)
y`<0 при x∈ (- ∞ ;1)
Функция убывает при x∈(- ∞ ;1)
7)y``=(4x^3-4)`=12x^2
y`` ≥ 0
функция выпукла вниз на (- ∞ ;+ ∞ )
Точек перегиба нет