Задача 62438 15-го декабря планируется взят кредит в...

61b1fb4c3cb287314c366465

26.12.2021 17:40:50

15-го декабря планируется взят кредит в банке на 1500000 на (n + 1) месяц. Условия его возврата таковы:

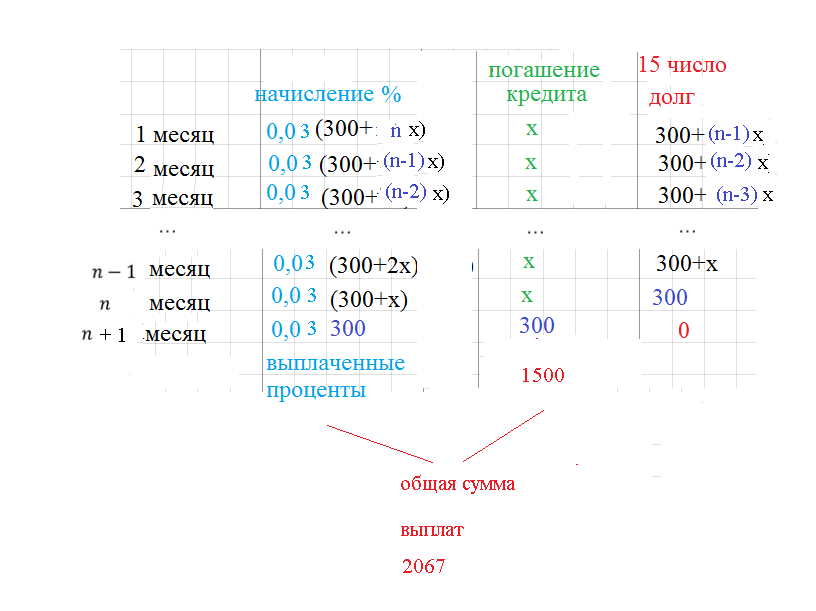
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по n-й долг должен быть на x тысяч рублей меньше долга на 15-е число предыдущего месяца;

— 15-го числа n-го месяца долг составит 300 тысяч рублей;

— к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.

Найдите x, если известно, что общая сумма выплат после полного погашения кредита составит 2067 тысяч рублей.

5f3ea7e3faf909182968ddd9

26.12.2021 19:44:15

★

Заполняем таблицу снизу вверх

Складываем столбик выплата кредита

nx+300=1500

nx=1200


2067-1500=567 - выплаченные проценты

Складываем столбик начисление процентов и приравниваем к числу 567

0,03*(300+nx)+0,03*(300+(n-1)x)+...+0,03*(300+x)+0,03*300=567

делим на 0,03

300+nx+300+(n-1)x+300+x+300=18900

300*(n+1)+x[m]\underbrace {(n+(n-1)+...+1)}_{сумма... n... членов ...арифметической... прогрессии }[/m]=18900

300*(n+1)+x*(n+1)*n/2=18900

Решаем систему уравнений:

{nx=1200 ⇒ x=1200/n и подставляем во второе уравнение
{300*(n+1)+x*(n+1)*n/2=18900

300*(n+1)+(1200/n)*(n+1)*(n/2)=18900

Делим на 300

n+1+2n+2=63

3n=60

n=20


x=1200/20=600

О т в е т.[red][b] 600 тыс.[/b][/red]