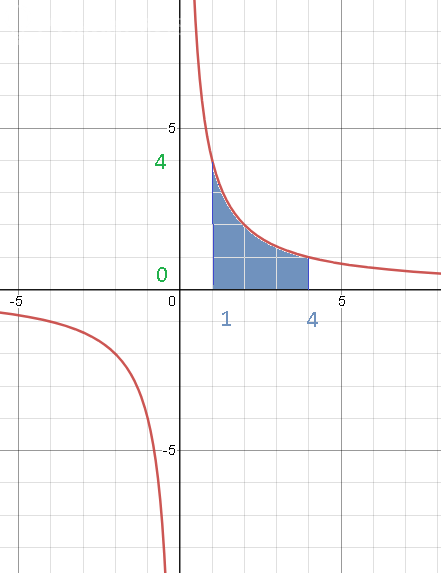
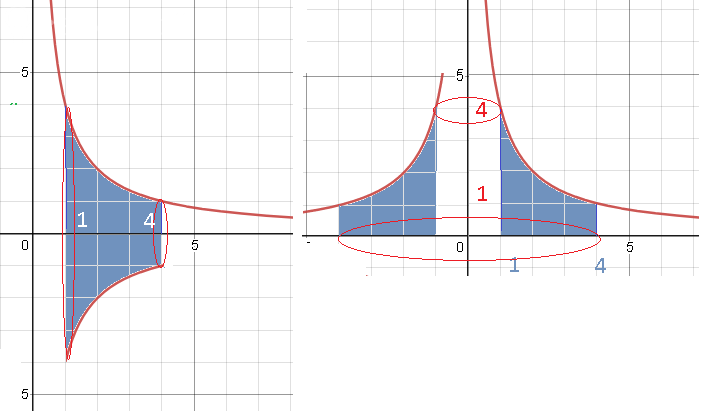
Задача 62160 Найти объемы тел, образованных при...

61b7b547852fab7de8442408

14.12.2021 00:05:28

Найти объемы тел, образованных при вращении вокруг осей Ох и Оу плоских фигур, ограниченных линиями y=4/x, x=1, x=4, y=0

5f3ea7e3faf909182968ddd9

14.12.2021 10:55:27

★

[m]V_{Ox}=π ∫ ^{4}_{1}(\frac{4}{x})^2dx=π ∫ ^{4}_{1}\frac{16}{x^2}dx=(-\frac{16}{x}|^{4}_{1}=π((-\frac{16}{4}-(-\frac{16}{1})=π(-4+16)=12π[/m]


[m]V_{Oy}=π ∫ ^{4}_{1}((\frac{4}{y})^2-1^2)dy+π ∫ ^{1}_{0}(4^2-1^2)dy=π(-\frac{16}{y}-y|^{4}_{1}=π(-\frac{16}{4}-4-(-\frac{16}{1}-1)+13π=π(-4-4+16+1)+13π=21π[/m]