Задача 62139 ...

61b748a7e1a86342357ca896

13.12.2021 16:31:19

a) Решите уравнение: 2sin^2x + sqrt(2)sin(x + π/4) = cos x

b) Укажите корни этого уравнения, принадлежащие отрезку [-2π; -π/2]

5f3ea7e3faf909182968ddd9

13.12.2021 18:41:55

★

Применяем формулу:

[r][m]sin( α + β )=sin α\cdot cos β +cos α\cdot sin β [/m][/r]

[m]2sin^2x+\sqrt{2}sinx \cdot cos\frac{π}{4}+\sqrt{2}cosx \cdot sin\frac{π}{4}=cosx[/m]


Так как [m]cos\frac{π}{4}=sin\frac{π}{4}=\frac{1}{\sqrt{2}}[/m]

[m]2sin^2x+sinx +cosx=cosx[/m]

[m]2sin^2x+sinx =0[/m]

[m]sinx(2sinx+1)=0[/m]

[m]sinx=0[/m] ИЛИ [m]2sinx+1=0[/m]

Решаем первое уравнение:

[m]sinx=0[/m] ⇒ [m] x=πn, n ∈ [/m][b] Z[/b]

Решаем первое уравнение:

[m]2sinx+1=0[/m] ⇒[m] sinx =-\frac{1}{2} ⇒ [m] x=(-1)^{k}arcsin(-\frac{1}{2})+πk, k ∈ [/m][b] Z[/b]

a)
О т в е т. [m] πn, n ∈ [/m][b] Z[/b]; [m] (-1)^{k}arcsin(-\frac{1}{2})+πk, k ∈ [/m][b] Z[/b].

б)
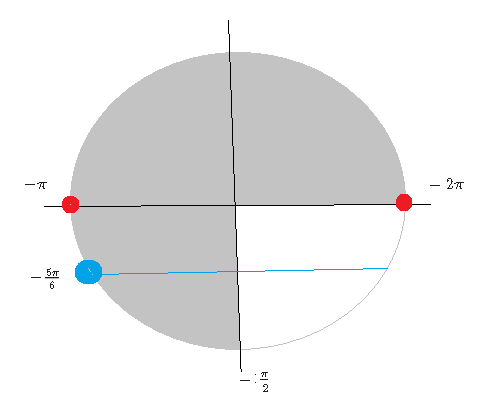
Отрезку [m][-2π; -\frac{π}{2}][/m] принадлежат корни:

[m]x_{1}=-2π[/m]

[m]x_{2}=-π[/m]

[m]x_{3}=-\frac{5π}{6}[/m]