Задача 62099 Разложить в ряд Фурье, заданную...
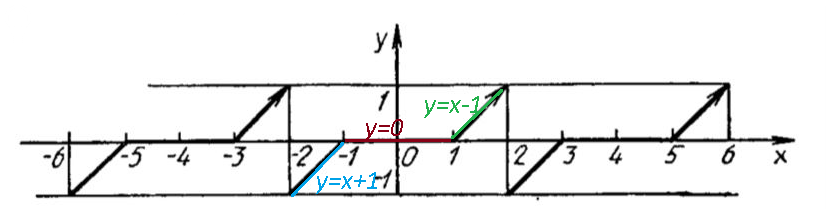
Условие
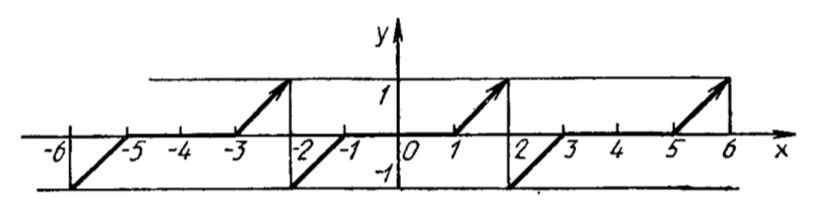
Решение
Нечетная.
Значит можно разложить в ряд по синусам на отрезке [-l;l]:
[m]f(x)= ∑ _{1}^{ ∞ }b_{n}sin\frac{π nx}{2}[/m]
[m] b_{n}=\frac{2}{l} ∫^{l}_{0}f(x)sin\frac{π nx}{2}dx=[/m]
l=2
так как
на [0;1]
f(x)=0;
на [1;2]
f(x)=x-1
[m]=\frac{1}{2} ∫^{2}_{1}(x-1)sin\frac{π nx}{2}dx=[/m]
считаем по частям
[m]u=x-1[/m] ⇒ [m]du=dx[/m]
[m]dv=sin\frac{π nx}{2}dx[/m] ⇒ [m]v= ∫ sin\frac{π nx}{2}dx=\frac{2}{πn} ∫ sin\frac{π nx}{2}d\frac{π nx}{2}=\frac{2}{πn}\cdot (-cos\frac{π nx}{2})[/m]
[m]∫^{2}_{1}(x-1)sin\frac{π nx}{2}dx=(x-1)\cdot\frac{2}{πn}\cdot (-cos\frac{π nx}{2})-∫^{2}_{1}\frac{2}{πn}\cdot (-cos\frac{π nx}{2})dx= [/m]считайте
Получаем
[m]f(x)= ∑ _{1}^{ ∞ }b_{n}sin\frac{π nx}{2}[/m]