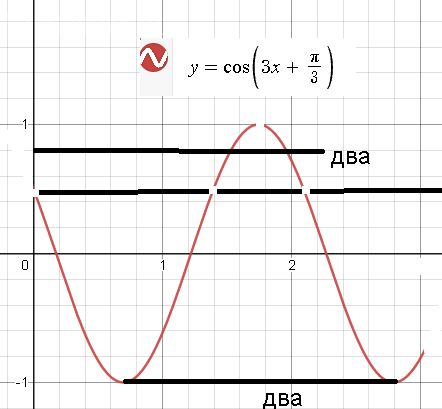
Задача 61600 Найти все значения параметра а ...

6035fc7016e9eb62f3f77539

17.11.2021 06:17:08

Найти все значения параметра а

5f3ea7e3faf909182968ddd9

17.11.2021 14:04:52

★

[m]f(0)=cos(3\cdot 0+\frac{π}{3})=cos\frac{π}{3}=\frac{1}{2}[/m]




[m]\frac{1}{2} < \frac{a}{3a+1}<1 [/m] или [m] \frac{a}{3a+1}=-1[/m]

⇒ решаем систему и уравнение и находим а




[m]\left\{\begin {matrix} \frac{a}{3a+1}<1\\\frac{a}{3a+1} >\frac{1}{2} \end {matrix}\right.[/m]⇒ [m](-1; -\frac{1}{2})[/m]


[m]\frac{a}{3a+1}+1=0[/m] ⇒ [m]a=-\frac{1}{4}[/m]


О т в е т. [m](-1; -\frac{1}{2})[/m]U{[m]-\frac{1}{4}[/m]}