Задача 61595 Найти все значения параметра а ...

6035fc7016e9eb62f3f77539

16.11.2021 21:21:41

Найти все значения параметра а

5f3ea7e3faf909182968ddd9

16.11.2021 21:39:02

★

[m]f(-\frac{π}{2})=3sin(2\cdot (-\frac{π}{2}-\frac{π}{6})=3sin(-π-\frac{π}{6})=\frac{3}{2}[/m]




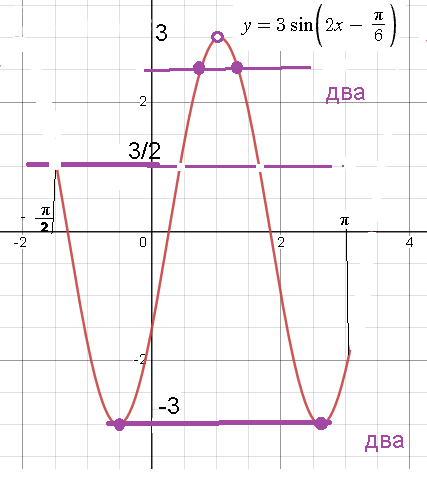
[m]\frac{3}{2} < \frac{a-2}{a+1}<3 [/m] или [m] \frac{a-2}{a+1}=-3[/m]

⇒ решаем систему и уравнение и находим а


[m]\left\{\begin {matrix} \frac{a-2}{a+1}<3\\\frac{a-2}{a+1} >\frac{3}{2} \end {matrix}\right.[/m]


[m]\left\{\begin {matrix} \frac{a-2}{a+1}-3<0\\\frac{a-2}{a+1} -\frac{3}{2} >0 \end {matrix}\right.[/m]


[m]\left\{\begin {matrix} \frac{a-2-3a-3}{a+1}<0\\\frac{2a-4-3a-3}{2(a+1)} >0 \end {matrix}\right.[/m]

[m]\left\{\begin {matrix} \frac{-2a-5}{a+1}<0\\\frac{-a-7}{2(a+1)} >0 \end {matrix}\right.[/m]

[m]\left\{\begin {matrix} a+1<0\\-2a-5 >0\\-a-7 <0 \end {matrix}\right.[/m] или [m]\left\{\begin {matrix} a+1>0\\-2a-5 <0\\-a-7 >0 \end {matrix}\right.[/m]

Вторая система не имеет решений.

⇒ [m](-7;-2,5)[/m]

[m] \frac{a-2}{a+1}=-3[/m] ⇒ [m] \frac{a-2}{a+1}+3=0[/m] ⇒ [m] \frac{a-2+3a+3}{2(a+1)}=0[/m] ⇒
[m] \frac{4a+1}{2(a+1)}=0[/m] ⇒ [m]a=-\frac{1}{4}[/m]

О т в е т. [m](-7;-2,5)[/m]U{[m]-\frac{1}{4}[/m]}