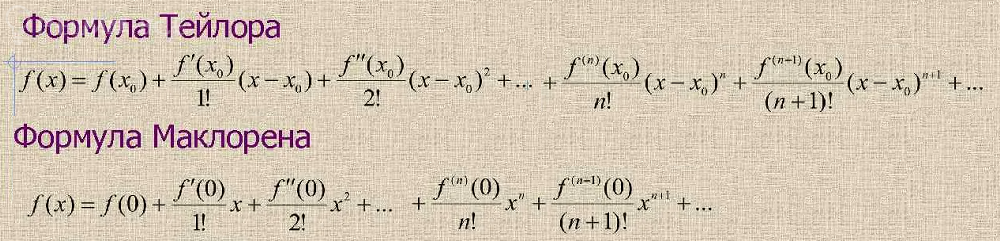Задача 61479 Нужно с помощью разложения в ряд найти...

618ca4f3c3f0ac1eb26b1cda

11.11.2021 08:09:46

Нужно с помощью разложения в ряд найти приближённо частное
решение дифференциального уравнения (определить пять отличных от нуля
членов разложения).

5f3ea7e3faf909182968ddd9

11.11.2021 11:01:25

★

y(0)=0,5 ⇒ x=0; y=0,5

y`=y^2+x^3

Подставляем координаты:

[b]y`(0)[/b]=0,5^2+0^3=[b]0,25[/b]


y``=(y`)`=(y^2+x^3)`=2y*y`+3x^2

[b]y``(0)[/b]=2*0,5*0,25+3*0^2=[b]0,25[/b]



y```=(y``)`=(2y*y`+3x^2)`=2*y`*y`+2y*y``+6x

y```(0)=2*0,25*0,25+2*0,5*0,25+6*0=0,125+0,25=0,375


y````=2*(y`*y`)`+2(y*y``)`+6=2y``*y`+2y`*y``+2y`*y``+2y*y```+6=6y`*y``+2y*y```+6

y````(0)=6*0,25*0,25+2*0,5*0,375+6=[b]&[/b]



y`````=(6y`*y``+2y*y```+6)`=6y``*y``+6*y`*y```+2y`*y```+2y*y````

y`````(0)=6*0,25*0,25+6*0,25*0,375+2*0,25*0,375+2*0,5*[b]&[/b]

считайте
и подставляйте найденные значения производных в формулу Тейлора.

Так как x_(o)=0, то эта формула Маклорена (ударение на о )
см вторую строчку в скрине