Задача 61472 Исследовать функцию y = f (x) на...

618c09aeb047e2547e5c4baa

10.11.2021 21:43:41

Исследовать функцию y = f (x) на непрерывность. Построить схематично график функции. Указать характер точек разрыва и величину скачка.

5f3ea7e3faf909182968ddd9

11.11.2021 00:22:12

★

На (- ∞ ;1) функция непрерывна, так как y=1-(x+1)^(2) непрерывна на (- ∞ ;+ ∞ )

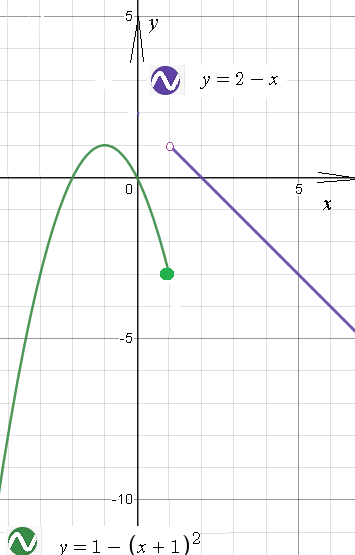
На (1;+ ∞ ) функция непрерывна, так как y=2-x непрерывна на (- ∞ ;+ ∞ )

Значит, надо выяснить непрерывность функции в точке

х=1

Находим предел слева:

lim_(x →1-0)f(x)=lim_(x →1 -0)(1-(x+1)^(2) )=1-(1+1)^1-4=-3

Находим предел справа:

lim_(x → 1+0)f(x)=lim_(x →1 +0)(2-x)=2-1=1

предел слева ≠ пределу справа



Функция имеет скачок ([i]конечный[/i]) в точке x=1
х=1 - [i]точка разрыва первого рода[/i]