Задача 61401 Проверить с помощью условий Коши-Римана,...
Условие
аналитической? w = z^2 Im z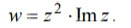
математика ВУЗ
2373
Решение
★
z^2=(x+iy)^2=x^2+i*2xy+(yi)^2=(x^2-y^2)+i*2xy
Imz=y
w=z^2*Imz=(x^2-y^2)y+i*2xy^2=(x^2y-y^3)+i*2xy^2
w=u+iv
u=x^2y-y^3
v=2xy^2
Находим
∂ u/ ∂ x=(x^2y-y^3)`_(x)=2xy+0=2xy
∂ u/ ∂ y=(x^2y-y^3)`_(y)=x^2-3y^2
∂ v/ ∂ x=(2xy^2)`_(x)=2y^2
∂ v/ ∂ y=(2xy^2)`_(y)=4xy
∂ u/ ∂ x ≠ ∂ v/ ∂ y
∂ u/ ∂ y ≠ -∂ v/ ∂ x
Не выполняются
Функция не является аналитической