Задача 61089 ...

616fbe698c4c5a5ade8be627

20.10.2021 10:01:17

Для треугольника ABC известно следующее: AB=8, BC=16, ∠ABC=120∘. Найдите R^2, где R — радиус наименьшего круга, в который можно поместить этот треугольник.

5f3ea7e3faf909182968ddd9

20.10.2021 12:14:52

★

По теореме косинусов:

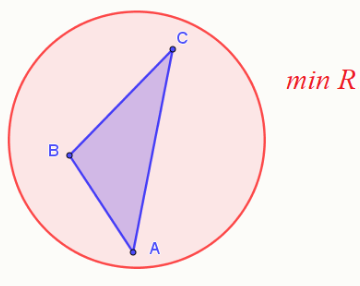
AC^2=AB^2+bC^2-2*AB*BC*cos ∠ ABC ⇒

AC^2=8^2+16^2-2*8*16*cos120 ° =64+256-2*8*16*(-1/2)=320+128=448

AC=sqrt(448)=sqrt(4*112)=sqrt(4*4*28)=sqrt(4*4*4*7)=8sqrt(7)


По теореме синусов

AC/sin ∠ ABC =2R

R=AC/2*sin120 ° =8sqrt(7)/sqrt(3)=8*sqrt(7/3) - минимальный радиус, это радиус описанной окружности.