Задача 60859 Решить вопрос о сходимости рядов; в е)...
Условие
абсолютно.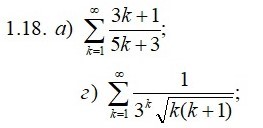
математика ВУЗ
497
Решение
★
[m]lim_{n → ∞ }a_{n}=lim_{n → ∞ }\frac{3n+1}{5n+3}=\frac{3}{5} ≠ 0[/m]
б) сходится по признаку Даламбера
[m]lim_{n → ∞ }\frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{1}{3^{n+1}\cdot \sqrt{(n+1)(n+2)}}}{\frac{1}{3^{n}\cdot \sqrt{n(n+1)}}}=lim_{n → ∞ }\frac{1}{3}\cdot \frac{\sqrt{n(n+1)}}{\sqrt{n+1}{n+2}}=\frac{1}{3}\cdot\frac{\sqrt{n(n+1)}}{\sqrt{n+1}{n+2}}=\frac{1}{3}\cdot 1=\frac{1}{3}<1[/m]