Задача 60822 Исследовать на сходимость два числовых...
Условие
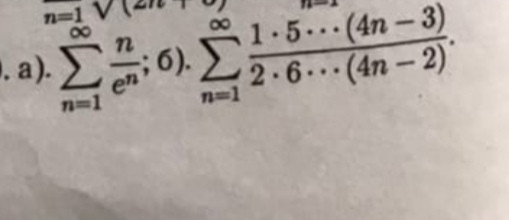
математика ВУЗ
525
Решение
★
Ряд сходится по признаку Даламбера
[m]lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{n+1}{e^{n}}}{\frac{n}{e^{n}}}=\frac{1}{e}lim_{n → ∞ }\frac{n+1}{n}=\frac{1}{e}\cdot 1=\frac{1}{e}<1[/m]
б)
Признак Даламбера
[m]lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{1\cdot 5\cdot ...\cdot (4n-3)(4(n+1)-3)}{2\cdot 6\cdot...\cdot (4n-2)(4(n+1)-2)}}{\frac{1\cdot 5\cdot ...\cdot (4n-3)}{2\cdot 6\cdot...\cdot (4n-2)}}=lim_{n → ∞ }\frac{4(n+1)-3}{4(n+1)-2}=1[/m]
ответа не дает.