Задача 60805 По алгоритму исследуйте функцию и...

614b4e9d7c1408291d40489d

22.09.2021 18:42:22

По алгоритму исследуйте функцию и постройте ее график у=3-2/х-1

5f3ea7e3faf909182968ddd9

22.09.2021 22:21:41

★

Область определения (– ∞;1)U(1;+ ∞ )

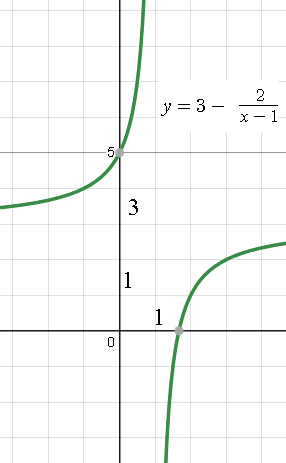
Прямая x=1 - вертикальная асимптота, так как lim_(x → 1)f(x)= ∞

Прямая y=3 - горизонтальная асимптота, так как lim_(x → ∞ )f(x)= 3


Функция не является ни чётной, ни нечётной

y(-x)=3-(2)/((-x)-1))=3+2/(х+1)

y(-x) ≠ y(x) и y(-x) ≠ -y(x)


Находим производную:

y`=(3)`-(2/(x-1))`=0-2*((x-1)^(-1))`=-2*(-1)*(x-1)^(-2)=2/(x-1)^2



y` > 0 на (– ∞;1) и y` > 0 на (1;+ ∞ )

Функция возрастает на (– ∞;1) и на (1;+ ∞ )

y` ≠ 0 ⇒ Нет точек экстремума

График см. рис.