Задача 60336 Исследовать функцию на непрерывность и...
Условие
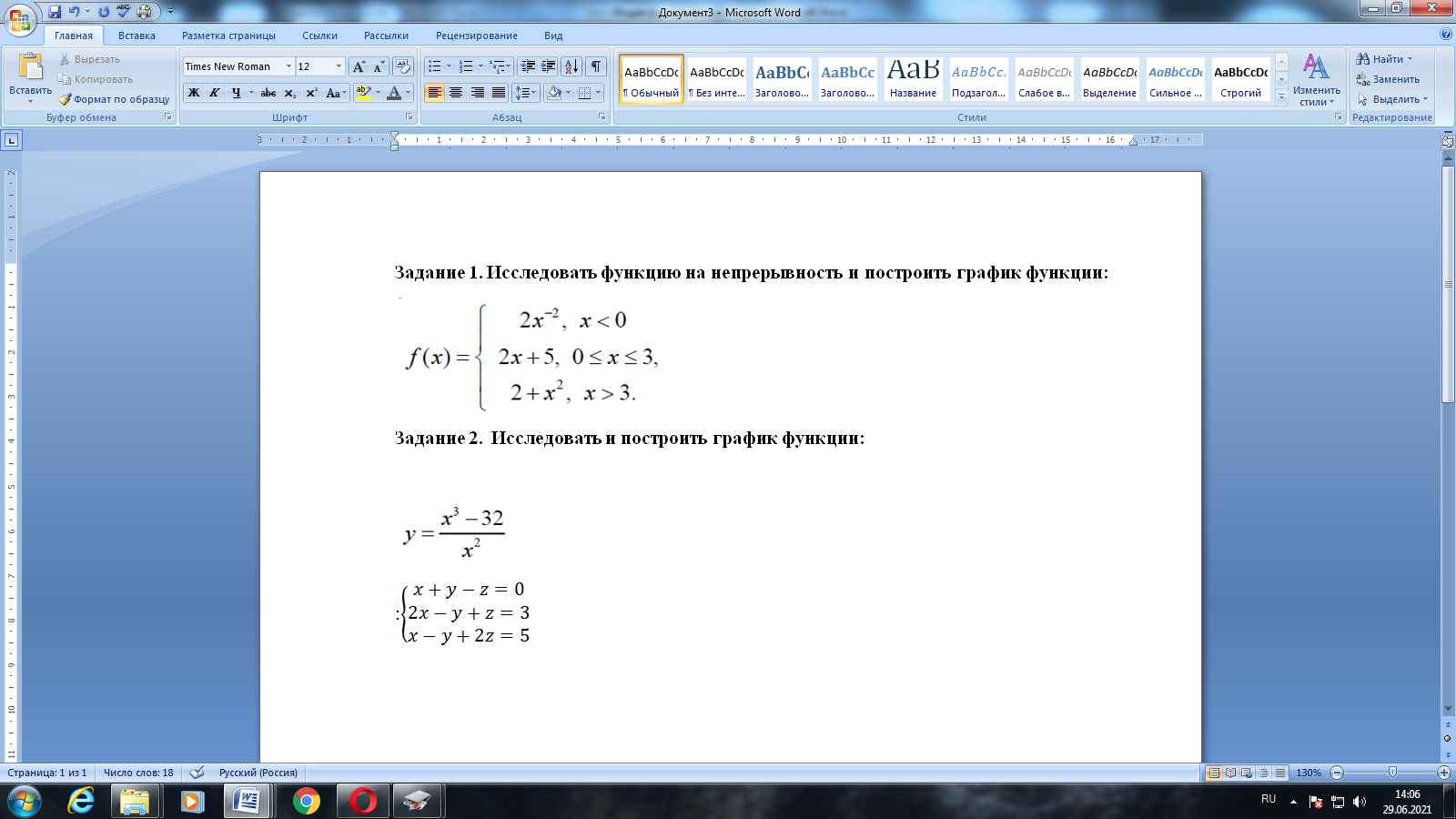
Решение
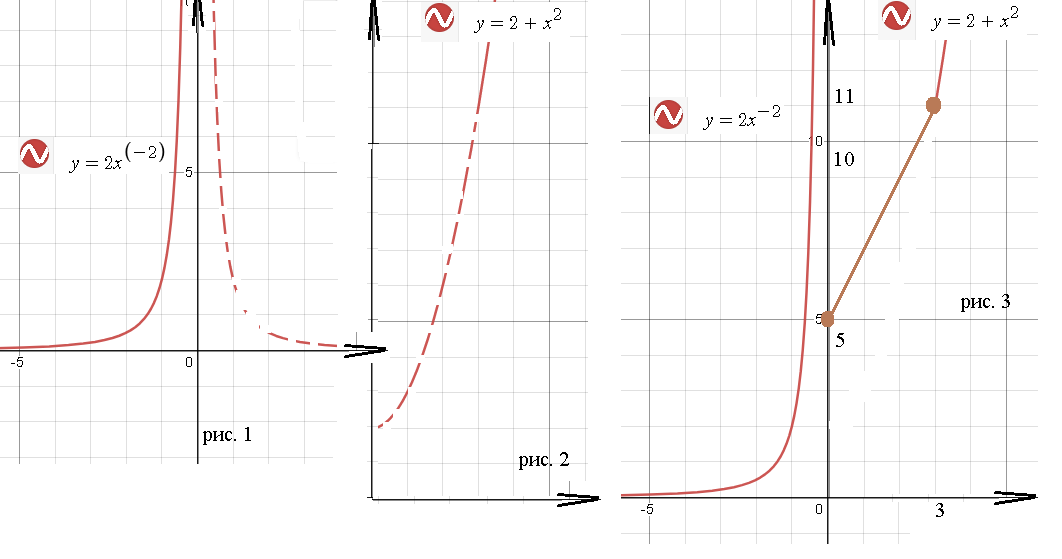
На (- ∞ ;0) функция непрерывна, так как y=2x^(-2) непрерывна на (- ∞ ;0) U (0;+ ∞ ) ( рис. 1)
На (0;3) функция непрерывна, так как y=2x+5 непрерывна на (- ∞ ;+ ∞ )
На (3;+ ∞ ) функция непрерывна, так как y=2+x^2 непрерывна на (- ∞ ;+ ∞ ) ( рис. 2)
Значит, надо выяснить непрерывность функции в точках
х=0 и х=2
Находим предел слева:
lim_(x → -0)f(x)=lim_(x → -0)2x^(-2)=2/(-0)^2=+ ∞
Функция имеет левосторонний [i]бесконечный[/i] предел. Значит х=0 - [i]точка разрыва второго рода[/i]
x=3
Находим предел слева:
lim_(x →3 -0)f(x)=lim_(x → 2-0)2x+5=2*(3-0)+5)=11
Находим предел справа:
lim_(x →3 +0)f(x)=lim_(x → 2+0)(2+x^2)=2+(3+0)^2=11
х=3 - [i]точка непрерывности [/i]
предел слева = пределу справа и равен значению функции в точке 2
f(3)=2*3+5=11
График на рис. 3