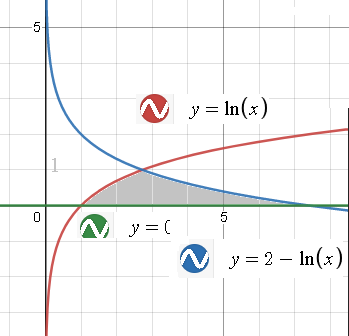Задача 60294 Найдите объём тела, полученного...

xnalio

23 июня 2021 г. в 04:18

Найдите объём тела, полученного вращением плоской фигуры вокруг оси.
Фигура ограничена линиями y=ln(x), y=2–ln(x), y=0, ось вращения OY

exponenta

23 июня 2021 г. в 15:34

★

[m]V_{Oy}=π ∫ ^{d}_{c}( g^2_{2}(y)-g^2_{1}(y))dy[/m]

d=1
c=0

y=lnx ⇒ x=e^y ⇒ ⇒ g₁(y)=e^y

y=2–lnx ⇒ lnx=2–y ⇒ e^2–y=x ⇒ g₂(y)=e^2–y


[m]V_{Oy}=π ∫ ^{1}_{0}( (e^{2-y})^2-(e^{y})^2)dy=π ∫ ^{1}_{0}( e^{2(2-y)}-e^{2y})dy=π(-\frac{1}{2}e^{4-2y}-\frac{1}{2}e^{2y})|^{1}_{0}=π(-\frac{1}{2}e^{2}-\frac{1}{2}e^{2})+π(\frac{1}{2}e^{4}+\frac{1}{2}e^{0})=π(\frac{e^4}{2}+1-e^2)[/m]