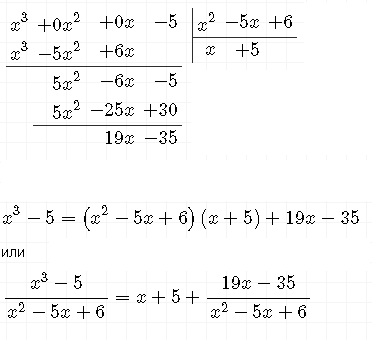Задача 60282 о<— ` =2 S ле o ХЕ ...
Условие
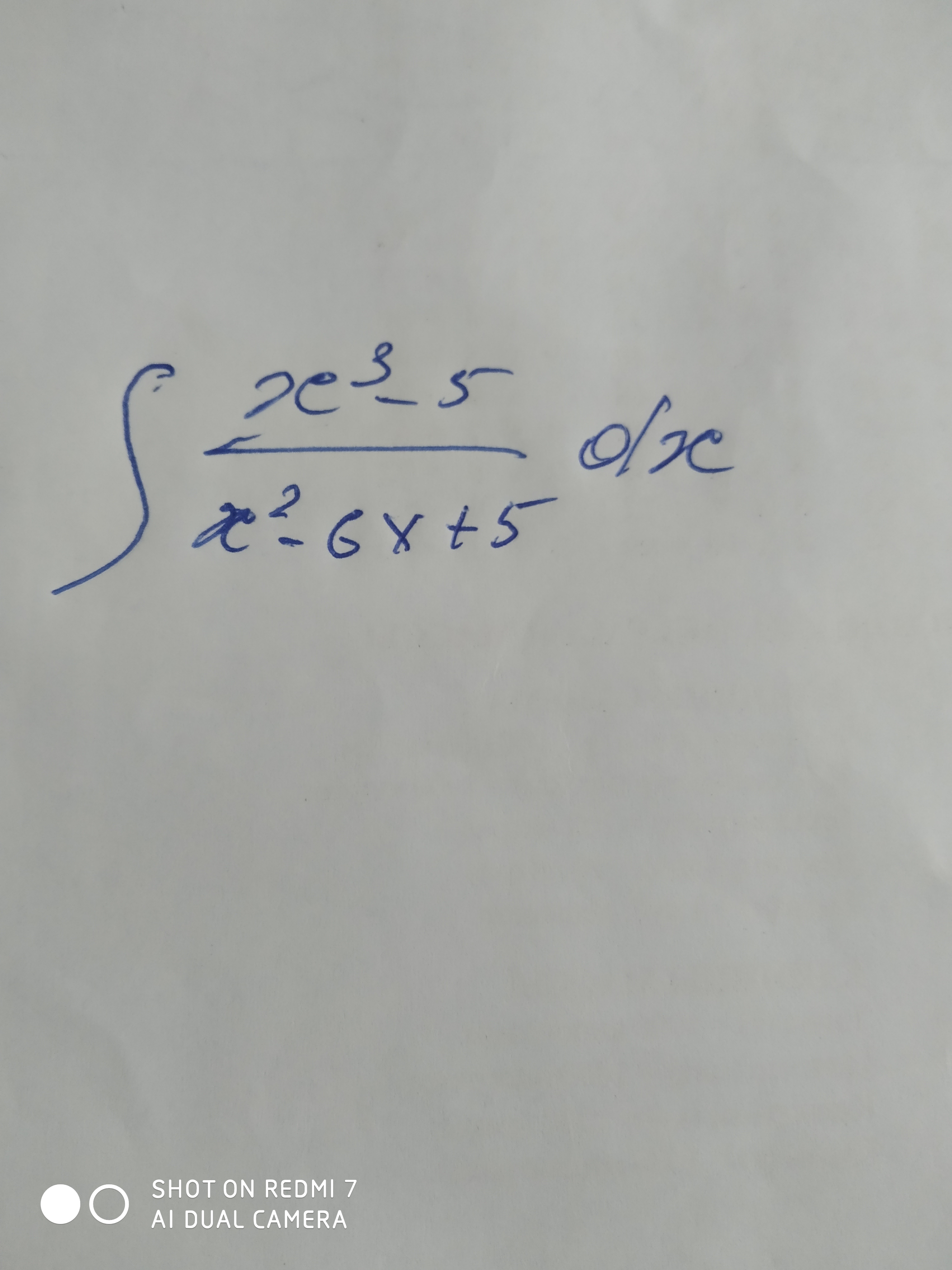
Решение
[m]\frac{x^3-5}{x^2-5x+6}=(x+5) +\frac{19x-35}{x^2-5x+6}[/m]
x^2-5x+6=(x-2)*(x-3)
Дробь[m] \frac{19x-35}{x^2-5x+6}[/m]
раскладываем на две простейшие дроби
[m] \frac{19x-35}{x^2-5x+6}=\frac{A}{x-2}+\frac{B}{x-3}[/m]
Приводим дроби справа в к общему знаменателю. Две дроби равны. Знаменатели равны.
Приравниваем числители:
[m]19x-35=A(x-3)+B(x-2)[/m]
Применяем[i] метод частных значений[/i].
При x=2
38-35=A(2-3)+B*0
A=-3
При х=3
19*3-35= А*0+B*1
B=22
[m] \frac{19x-35}{x^2-5x+6}=-\frac{3}{x-2}+\frac{22}{x-3}[/m]
Интеграл от суммы равен сумме интегралов
[m] ∫\frac{x^3-5}{x^2-5x+6}dx= ∫ (x+5)dx- ∫\frac{19x-35}{x^2-5x+6}dx=∫ (x+5)dx- ∫ \frac{3}{x-2}dx+ ∫ \frac{22}{x-3}dx=[/m]
=[b](x^2/2)+5x-3ln|x-2|+22ln|x-3|+C [/b]
=============