Задача 60243 1. Могут ли быть перпендикулярны к одной...

60812b00031948747667c36b

13.06.2021 15:15:54

1. Могут ли быть перпендикулярны к одной плоскости две стороны: 1) треугольника; 2) трапеции; 3) правильного шестиугольника?
2. Каково взаимное расположение двух плоскостей, если известно, что только одна из них перпендикулярна данной прямой?
3. Прямая перпендикулярна к одной из двух пересекающихся плоскостей. Может ли она быть перпендикулярной другой плоскости?
4. Прямая MB перпендикулярна к сторонам AB и BC треугольника ABC. Определите вид треугольника MBD, где D – произвольная точка прямой AC.

5f3ea7e3faf909182968ddd9

13.06.2021 21:30:47

★

1. Могут ли быть перпендикулярны к одной плоскости две стороны:


1) треугольника;
Нет, если две стороны перпендикулярны, то и третья перпендикулярна



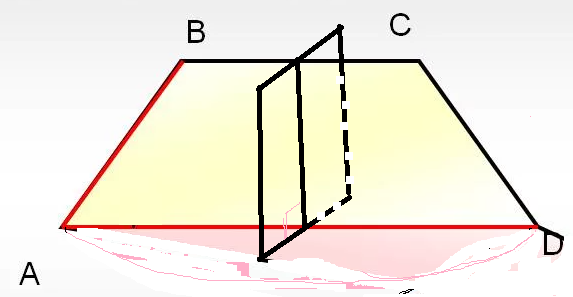
2) трапеции

Могут, параллельные стороны трапеции


3) правильного шестиугольника

могут, параллельные стороны шестиугольника


2. Каково взаимное расположение двух плоскостей, если известно, что только одна из них перпендикулярна данной прямой?

Плоскости пересекаются и даже могут быть перпендикулярными.

3. Прямая перпендикулярна к одной из двух пересекающихся плоскостей.
Может ли она быть перпендикулярной другой плоскости?


4. Прямая MB перпендикулярна к сторонам AB и BC треугольника ABC. Определите вид треугольника MBD, где D – произвольная точка прямой AC.

Прямоугольный.

Прямая MB перпендикулярна к двум пересекающимся сторонам AB и BC треугольника ABC ⇒ Прямая MB перпендикулярна плоскости треугольника ABC ⇒ Прямая MB перпендикулярна любой прямой, лежащей в плоскости треугольника ABC ⇒

Прямая MB перпендикулярна BD