Задача 60227 Исследовать функцию на непрерывность и...
Условие

Решение
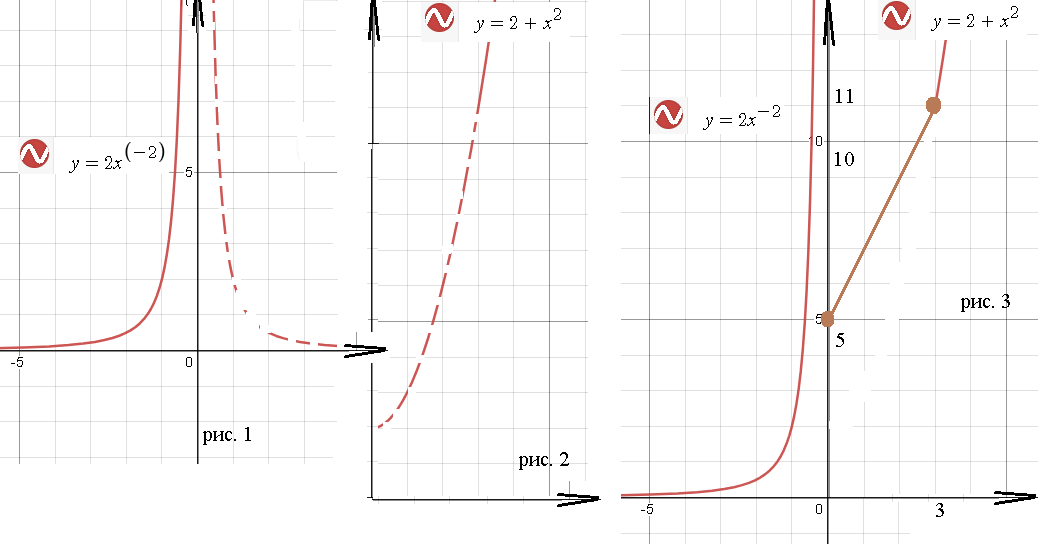
На (- ∞ ;0) функция непрерывна, так как y=2x^(-2) непрерывна на (- ∞ ;0) U (0;+ ∞ ) ( рис. 1)
На (0;3) функция непрерывна, так как y=2x+5 непрерывна на (- ∞ ;+ ∞ )
На (3;+ ∞ ) функция непрерывна, так как y=2+x^2 непрерывна на (- ∞ ;+ ∞ ) ( рис. 2)
Значит, надо выяснить непрерывность функции в точках
х=0 и х=2
Находим предел слева:
lim_(x → -0)f(x)=lim_(x → -0)2x^(-2)=+ ∞
Функция имеет левосторонний [i]бесконечный[/i] предел. Значит х=0 - [i]точка разрыва второго рода[/i]
x=3
Находим предел слева:
lim_(x →3 -0)f(x)=lim_(x → 2-0)(2*3+5)=11
Находим предел справа:
lim_(x →3 +0)f(x)=lim_(x → 2+0)(2+3^2)=11
х=3 - [i]точка непрерывности [/i]
предел слева = пределу справа и равен значению функции в точке 2
f(3)=2*3+5=11
2.
Область определения (- ∞ ;0)U(0;+ ∞ )
Функция не является ни чётной, ни нечётной, ни периодической
Область определения симметрична относительно 0 , но
[m] y(-x)=\frac{ (-x)^3-32}{(-x)^2}=-\frac{-x^3-32}{x^2}[/m]
[m]y(-x) ≠ y(x)[/m] и [m]y(-x) ≠- y(x)[/m]
Прямая [m] x=0 [/m] является [i] вертикальной[/i] асимптотой.
Так как [m] lim_{x → -0}\frac{ x^3-32}{x^2}=+ ∞ [/m]
[i]Горизонтальных[/i] асимптот нет, так как
[m] lim_{x → ∞}\frac{ x^3-32}{x^2}= ∞ [/m]
Наклонная асимптота:
[m] k= lim_{x → ∞}\frac{f(x)}{x}=lim_{x → ∞}\frac{ x^3-32}{x\cdot x^2}= 1 [/m]
[m]k=1 [/m]
[m]b= lim_{x → ∞}(\frac{ x^3-32}{x^2}- x)= lim_{x → ∞}\frac{x^3-32-x^3}{x^2}= lim_{x → ∞}\frac{(-32)}{x^2}=0[/m]
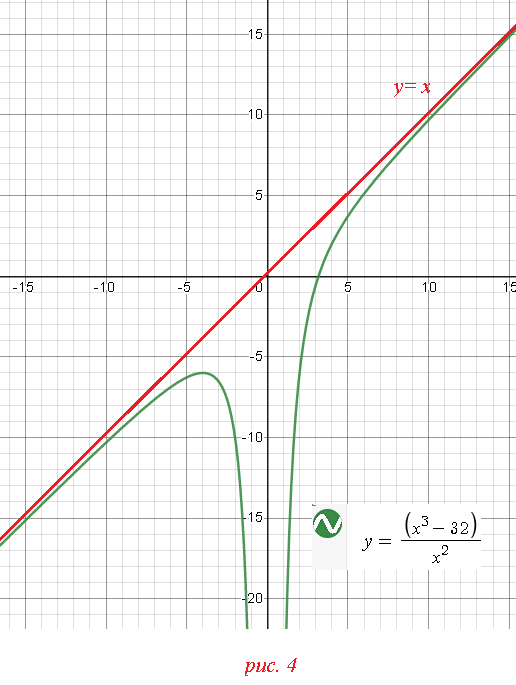
[m]y=x-0 [/m]⇒y=x[/m] [i]- наклонная асимптота[/i].
[b]Исследование с помощью первой производной[/b]:
[m]y`=\frac{3x^2\cdot x^2-(x^3-32)\cdot 2x}{(x^2)^2}[/m]
[m]y`=\frac{3x^4-2x^4+64x\cdot 2x}{(x^2)^2}[/m]
[m]y`=\frac{x^4+64x}{x^4}[/m]
[m]y`=\frac{x^3+64}{x^3}[/m]
y`=0
x=-4
Расставляем знак производной на ОДЗ:
___-___ (-4) ____+__ (0) ___+__
y`>0 на (-4;0) и на (0;+ ∞ )
Значит функция [i]возрастает[/i] на (-4;0) и на (0;+ ∞ )
y`<0 на (-∞;-4)
Значит, функция [i] убывает [/i] на(-∞;-4)
x=-4 - точка максимума, производная меняет знак с + на -
[m]y(-4)=\frac{(-4)^3-32}{(-4)^2}=-6[/m]
[b]Исследование с помощью второй производной:[/b]
[m]y``=(y`)`=(\frac{x^3+64}{x^3})`=(1+64x^{-3})`=0+64\cdot (-3)\cdot x^{-4}[/m]
[m]y``=-192\frac{1}{x^4}[/m]
[m]y`` <0 [/m] на (- ∞ ; -3) и (-3;0) и на ( 0;+ ∞ ) ⇒ функция выпукла вверх на на (- ∞ ; -3) и (-3;0) и на ( 0;+ ∞ )
Точек перегиба нет
График на рис. 4