Задача 60149 Разложить данную функцию f(x) в ряд...
Условие
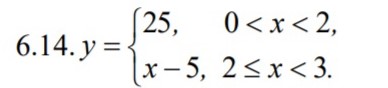
Решение
Продолжить функцию на (-3;3) можно[i] чётным [/i]образом, тогда получим разложение в ряд Фурье по косинусам:
[m]\frac{a_{o}}{2}+ ∑_{1}^{ ∞}a_{n} cos\frac{nπx}{3}[/m]
[m]a_{o}=\frac{2}{3} ∫_{0} ^{3}f(x)dx=\frac{2}{3} ∫_{0} ^{2}25dx+\frac{2}{3} ∫_{2} ^{3}(x-5)dx=[/m]
[m]a_{n}=\frac{2}{3} ∫_{0} ^{3}f(x)cos\frac{nπx}{3}dx=\frac{2}{3} ∫_{0} ^{2}25cos\frac{nπx}{3}dx+\frac{2}{3} ∫_{2} ^{3}(x-5)cos\frac{nπx}{3}dx=[/m]
Можно продолжить функцию на (-3;3)[i] нечётным [/i]образом, тогда получим разложение в ряд Фурье по синусам:
[m] ∑_{1}^{ ∞}и_{n} sin\frac{nπx}{3}[/m]
[m]b_{n}=\frac{2}{3} ∫_{0} ^{3}f(x)sin\frac{nπx}{3}dx=\frac{2}{3} ∫_{0} ^{2}25sin\frac{nπx}{3}dx+\frac{2}{3} ∫_{2} ^{3}(x-5)sin\frac{nπx}{3}dx=[/m]