Задача 60144 Исследовать сходимость знакопеременных...
Условие
сходится, то определить, сходится он абсолютно или условно.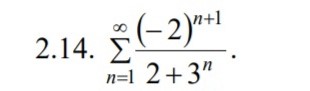
математика ВУЗ
575
Решение
★
[m]|a_{n}|=\frac{2^{n+1}}{2+3^{n}}[/m]
Ряд из модулей сходится по признаку Даламбера
[m]lim_{n → ∞ }\frac{|a_{n+1}|}|{a_{n}|}=lim_{n → ∞ }\frac{\frac{2^{n+2}}{2+3^{n+1}}}{\frac{2^{n+1}}{2+3^{n}}}=[/m]
[m]=lim_{n → ∞ }\frac{2^{n+2}\cdot (2+3^{n})}{(2+3^{n+1})\cdot 2^{n+1}}=lim_{n → ∞ }\frac{2(2+3^{n}}{2+3^{n+1}}=\frac{ ∞ }{ ∞ }[/m]
Делим и числитель и знаменатель на [m]3^{n+2}[/m]
[m]=lim_{n → ∞ }\frac{\frac{2(2+3^{n}}{3^{n+1}}{\frac{2+3^{n+1}}{3^{n+1}}=\frac{2}{3} < 1[/m]
Значит, данный ряд сходится абсолютно.