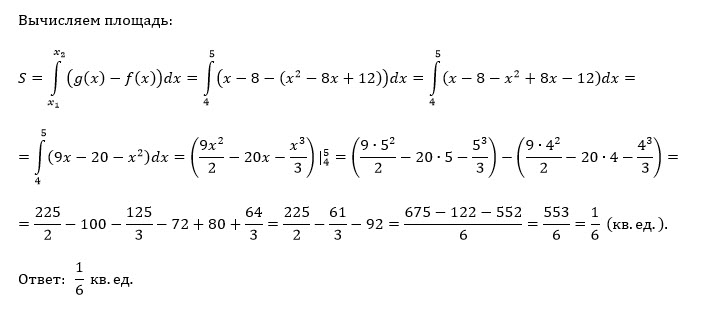Задача 60084 Вычислить площадь фигуры, ограниченной...
Условие
математика ВУЗ
2950
Решение
★
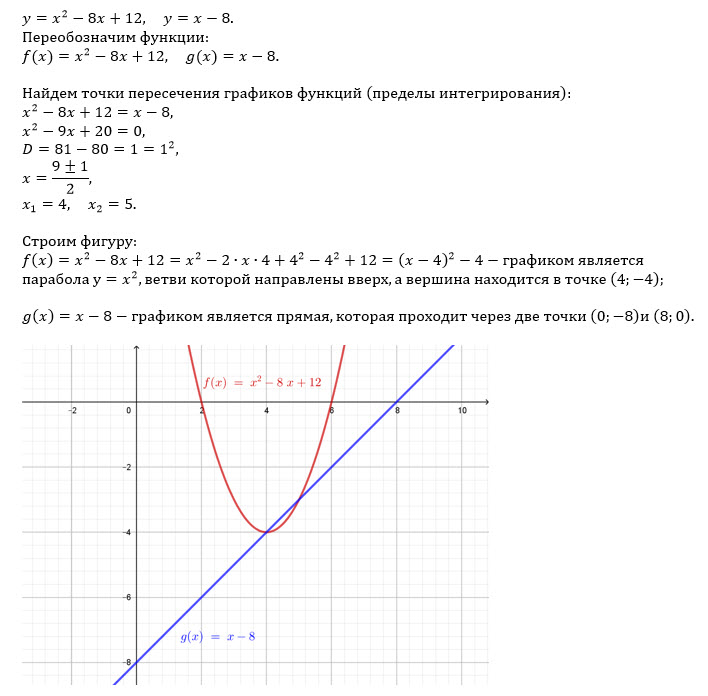
Строим графики функций y=f(x) и y=g(x)
f(x)=x^2-8x+12
g(x)=x-8
cм. рис.
Находим абсциссы точек пересечения графиков:
[m] x^2-8x+12=x-8[/m]
[m] x^2-9x+20=0[/m]
D=81-80=1
x_(1)=4; x_(2)=5
[m]S= ∫_{4} ^{5}(x-8-(x^2-8x+12))dx=∫_{4} ^{5}(9x-x^2-20)dx=(9\frac{x^2}{2}-\frac{x^3}{3}-20x)|_{4} ^{5}=(9\frac{5^2}{2}-\frac{5^3}{3}-20\cdot 5)-(9\frac{4^2}{2}-\frac{4^3}{3}-20\cdot 4)=[/m]
[m]=\frac{9}{2}\cdot (25-16)-\frac{5^3-4^3}{3}-20\cdot (5-4)=\frac{81}{2}-\frac{61}{3}-20=\frac{243-122}{6}-20=\frac{121}{6}-20=\frac{1}{6}[/m] 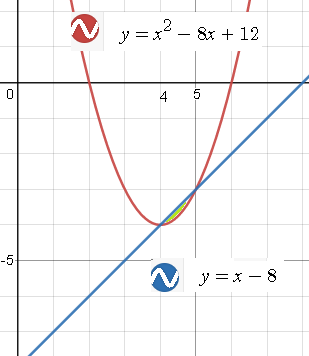
Все решения