Задача 59987 ...

60b160bea1c50e1d30437929

29.05.2021 00:31:05

Основание прямой призмы АВСА1В1С1 – прямоугольный треугольник, катеты ВС и АС которого равны 2√6. Плоскость АВС1 наклонена к плоскости основания под углом 30⁰. Найдите площадь сечения.

5f3ea7e3faf909182968ddd9

29.05.2021 09:47:24

★

треугольник АВС - прямоугольный, , катеты ВС и АС равны 2√6.

Тогда

AB^2=AC^2+BC^2=(2sqrt(6))^2+(2sqrt(6))^2=24+24=48

AB=4sqrt(3)

CН= AC*BC/AB=2sqrt(6)*2sqrt(6)/4sqrt(3)=2sqrt(3)

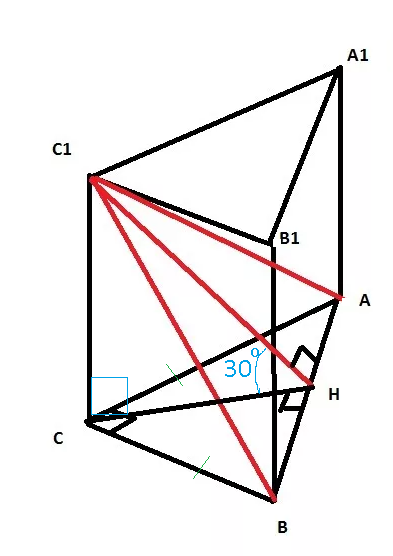
Из прямоугольного Δ С_(1)СН с углом в 30 °

сos ∠ С_(1)НC=CH/C_(1)H


С_(1)Н=CH/cos30 °= 2sqrt(3)/sqrt(3)/2=4


S_(сечения)=S_( Δ ABC_(1)=(1/2)AB*C_(1)H=(1/2)*4sqrt(3)*4=[b]8sqrt(3)[/b]