Задача 59962 2log5(xsqrt(2))-log5(x/(1-x)) <=...
Условие
Решение
[m]\left\{\begin {matrix}x\sqrt{2}>0\\\frac{x}{1-x}>0\\22x^2+\frac{1}{x}-12 >0\end {matrix}\right.[/m][m]\left\{\begin {matrix}x>0\\1-x>0\\22x^2+\frac{1}{x}-12 >0\end {matrix}\right.[/m][m]\left\{\begin {matrix}0<x<1\\22x^2>12-\frac{1}{x} \end {matrix}\right.[/m]
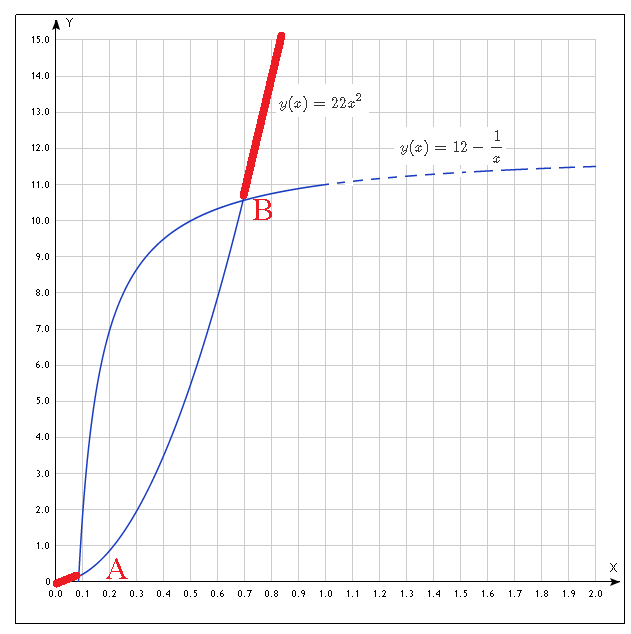
Cм. графическое решение неравенства ( две точки пересечения А и В):
[b]0 < x < x_(A); x_(B) < x < 1[/b]
Как найти значения x_(A) и x_(B) - решить кубическое уравнение:
22x^3-12x+1=0 ( см. решение кубических уравнений в радикалах)
А можно и не решать.
См. объяснение этому в конце решения задачи.
Далее свойства логарифмов:
[m]log_{a}b^{k}=klog_{a}b[/m] . [b] b>0[/b]; a>0; a ≠ 1
[m]log_{5}x\sqrt{2}=log_{5}x^2\cdot2=log_{5}2x^2[/m]
Тогда неравенство принимает вид:
[m]log_{5}2x^2 ≤ log_{5}\frac{x}{1-x}+log_{5}(22x^2+\frac{1}{x}-12)[/m]
Применяем свойство логарифмов : [m]lg(x\cdot y)=lgx+lgy[/m], которое верно при x>0; y>0
справа налево
[m]log_{5}2x^2 ≤ log_{5}\frac{x}{1-x}\cdot (22x^2+\frac{1}{x}-12)[/m]
Логарифмическая функция с основанием 5 монотонно возрастающая, значит
бОльшему значению функции соответствует бОльшее значение аргумента
[m]2x^2 ≤ \frac{x}{1-x}\cdot (22x^2+\frac{1}{x}-12)[/m]
- дробно рациональное неравенство.
так как (1-x) >0
умножаем обе части неравенства на положительное выражение, знак неравенства сохраняется
[m]2x^2(1-x) ≤ 22x^3-12x+1[/m]
[m]24x^3-2x^2-12x+1 ≥ 0[/m]
[m]2x^2(12x-1)-(12x-1)≥ 0[/m]
(12x-1)(2x^2-1) ≥ 0
Решаем неравенство методом интервалов на ОДЗ.
x=1/12; x=-1/sqrt(2); x=(1/sqrt(2))
x=-1/sqrt(2) не входит в ОДЗ
(0) ____+_____ [1/12] _________-___________ [1/sqrt(2)] ____+____ (1)
x=1/sqrt(2) входит в ОДЗ, так как 22*(1/sqrt(2))^2+sqrt(2)-12 >0 верно.
x=1/12 входит в ОДЗ, так как 22*(1/144) +12 -12 >0 верно
[red]x_(A) > 1/12[/red]
[red]x_(B)<1/sqrt(2)[/red]
((0) ____[red]+[/red]_____ [1/12] __ [red]+[/red]___ ([b]x_(A) [/b]) ____-___ [b](x_(B)[/b]) ___[red]+[/red]____ [1/sqrt(2)] ____[red]+[/red]____ (1)
[b]Ответ[/b] с учетом ОДЗ
[b](0;1/12] U [1/sqrt(2);+ ∞ )[/b]