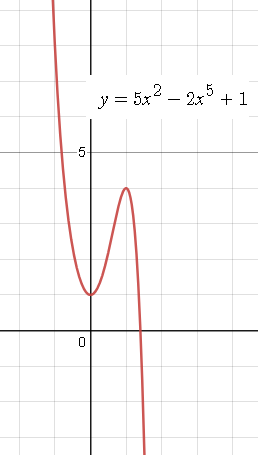
Задача 59938 Исследовать график функции y=5x^2-2x^5+1...
Условие
Решение
y`=10x-10x^4
y`=0
10x-10x^4=0
10x*(1-x^3)=0
x_(1)=0; x_(2)=1
Знак производной:
__-__ (0) __+___ (1) __-__
y`>0 на (0 ;1) , значит функция [blue][i]возрастает[/i] [/blue] на (0;1)
y`< 0 на (- ∞ ;0) и на (1;+ ∞) , значит функция[blue][i] убывает[/i][/blue] на (- ∞ ;0) и на (1;+ ∞)
х=1 - точка[i] максимума[/i], производная меняет знак с + на -
y(1)=5-2+1=4
х=0 - точка[i] минимума[/i], производная меняет знак с - на +
у(0)=1
y``=(10x-10x^4)`=10-40x^3
y``=0
10-40x^3=0
x^3=1/4
x=∛(1/4)- точка перегиба, вторая производная меняет знак с + на -
Функция выпукла вниз на ( (- ∞ ;∛(1/4)) и выпукла вверх на (∛(1/4);+ ∞ )
См. график на рис.