Задача 59785 вычислить площадь фигуры ограниченной...
Условие
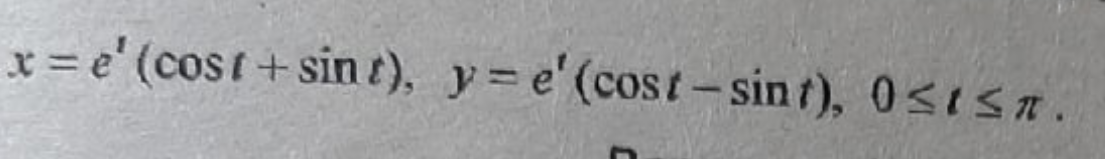
Решение
x`(t)=e^(t)*(cost+sint)+e^(t)*(-sint+cost)=e^(t)*(2cost)
y`(t)=e^(t)*(cost-sint)+e^(t)*(-sint-cost)=e^(t)*(-2sint)
При t=0 ⇒ x=1
При t=π ⇒ x=-e^(π)
[a;b]=[-e^(π); 1]
⇒
α =π
β =0
S= ∫_(π) ^(0)e^(t)*(cost-sint)*e^(t)*(2cost)dt=
считаем по частям каждый из двух интегралов два раза....
В данной задаче удобнее применить вторую формулу ( выделена красным цветом)
S= (1/2)∫_(π) ^(0)(e^(t)*(cost+sint)*e^(t)*(-2sint)-e^(t)*(cost-sint)*e^(t)*(2cost))dt=
=-(1/2)∫_(0) ^(π)(e^(t))^(2)*(-2sint*cost-2sin^2t-2cos^2t+2sint*cost)dt=
=-(1/2)∫_(0) ^(π)(e^(t))^(2)(-2)dt=
=∫_(0) ^(π)e^(2t)dt=(1/2)e^(2t)|_(0)^(π)=(1/2)e^(2π)-(1/2)e^(0)=[b](1/2)*(e^(2π)-1)[/b]

