Задача 59784 Вычислить площадь фигуры ограниченный...

609fcb343f1bb8747d24c8d8

15.05.2021 16:30:09

Вычислить площадь фигуры ограниченный линии f(x)= x+5;g(x)=x^2-4x+5;x=-3,x=3;y=0.

5f3ea7e3faf909182968ddd9

15.05.2021 17:36:41

★

Найдем абсциссы точек пересечения графиков

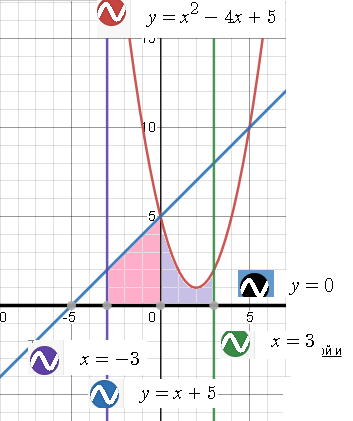
y=x+5 и y=x^2-4x+5

x^2-4x+5=x+5

x^2-5x=0

x*(x-5)=0

x=0 или x=5



Фигура состоит из двух криволинейных трапеций ( cм. рис.)

[m]S=S_{1}+S_{2}= ∫_{-3}^{0}(x+5)dx+ ∫_{0}^{3}(x^2-4x+5)dx=(\frac{x^2}{2}+5x) |_{-3}^{0}+(\frac{x^3}{3}-4\cdot \frac{x^2}{2}+5x)|_{0}^{3}=0-(\frac{(-3)^2}{2}+5\cdot (-3))+(\frac{3^3}{3}-4\cdot \frac{3^2}{2}+5\cdot 3-0)=[/m]