Задача 59746 Исследовать на сходимость числовые ряды....
Условие
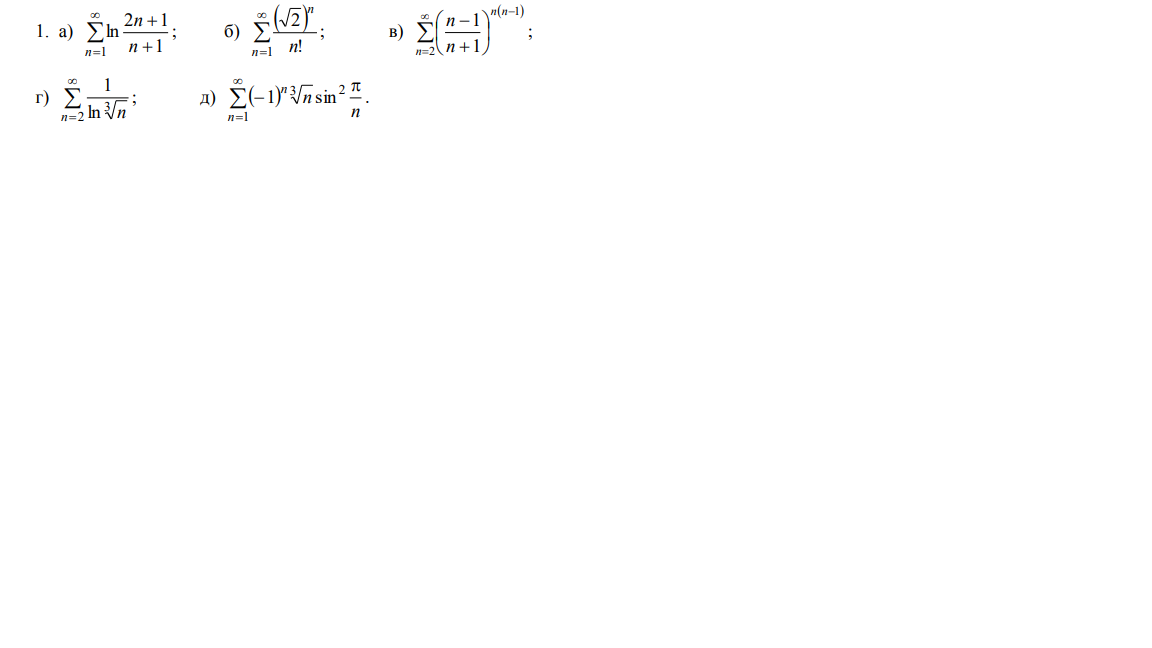
математика ВУЗ
615
Решение
★
Применяем признак Даламбера
[m]a_{n}=\frac{(\sqrt{2})^{n}}{n!}[/m]
[m]a_{n+1}=\frac{(\sqrt{2})^{n+1}}{(n+1)!}[/m]
[m]lim_{n→ ∞}\frac{a_{n+1}}{a_{n}}=lim_{n→ ∞}\frac{\frac{(\sqrt{2})^{n+1}}{(n+1)!}}{\frac{(\sqrt{2})^{n}}{n!}}=[/m]
[m]=lim_{n→ ∞}\frac{(\sqrt{2})^{n+1}\cdot n!}{(n+1)!\cdot (\sqrt{2})^{n}}=lim_{n→ ∞}\frac{\sqrt{2}}{n+1}=0 <1[/m]
По признаку Даламбера ряд сходится