Задача 59037 xy' = y - xe^(y/x);...
Условие
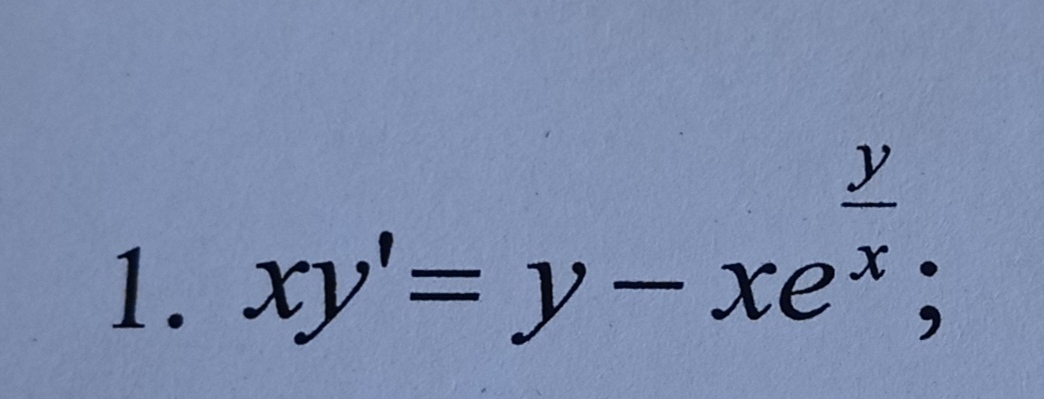
математика ВУЗ
521
Решение
★
y`=(y/x)-e^(y/x)
Это однородное
Решаем заменой
(y/x)=u
y=x*u
y`=u+xu`
u+xu`=u-e^(u)
xu`=-e^(u) - уравнение с разделяющимися переменными
u`=du/dx
xdu=-e^(u)dx - разделяем переменные
e^(u)du=-dx/x
Интегрируем
∫ e^(u)du=- ∫ dx/x
e^(u)=-ln|x|+lnC
e^(u)=lnC/|x|
u=ln(lnC/|x|)
Обратный переход
(y/x)=ln(lnC/|x|)
y=x*ln(lnC/|x|) - о т в е т
