Задача 58327 ...

604209edc87bcc1c7d52274c

05.03.2021 14:57:17

a) Решите уравнение cos2x + √2cos(π/2 - x) - 1 = 0.

б) Укажите корни этого уравнения, принадлежащие отрезку [5π/2 ; 4π].

5f3ea7e3faf909182968ddd9

05.03.2021 15:07:39

★

Применяем [i]формулы приведения[/i].

[m]cos2x+\sqrt{2}\cdot (sinx)-1=0[/m]

Применяем [i]формулу косинуса двойного угла[/i] и тригонометрическую единицу:


[m]cos^2x-sin^2x+\sqrt{2}\cdot sinx-cos^2x-sin^2x=0[/m]

[m]\sqrt{2}\cdot sinx-2sin^2x=0[/m]

Раскладываем на множители:

[m]sinx \cdot (\sqrt{2}-2sinx)=0[/m]

[m] sinx=0 [/m] или [m] \sqrt{2}-2sinx=0[/m]

[m] sinx=0 [/m] или [m] sin x =\frac{\sqrt{2}}{2}[/m]

[m] x =πn, n ∈ [/m] [b]Z[/b] или [m] x=(-1)^{k}arcsin\frac{\sqrt{2}}{2}+πk, k ∈ [/m] [b]Z[/b]
[m] x =πn, n ∈ [/m] [b]Z[/b] или [m]x= (-1)^{k}\frac{π}{4}+πk, k ∈ [/m] [b]Z[/b]

О т в е т. [m] x =πn, n ∈ [/m][b]Z[/b] или [m]x= (-1)^{k}\frac{π}{4}+πk, k ∈ [/m][b]Z[/b]

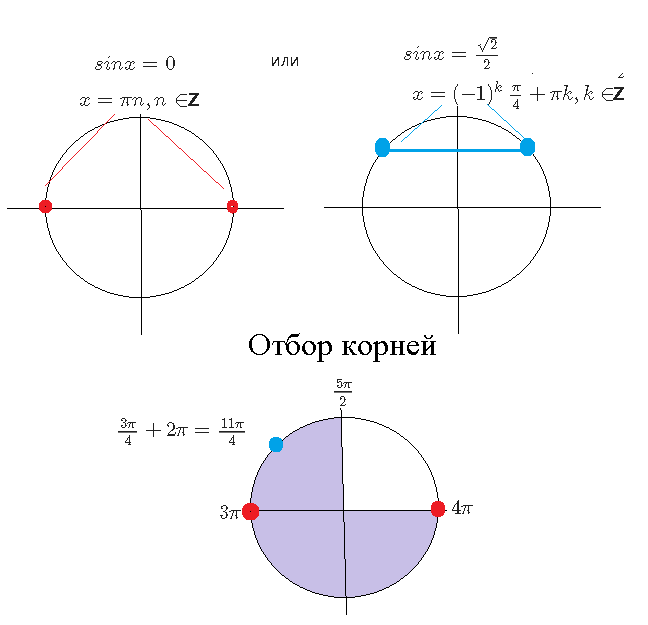
Отрезку [m][\frac{5π}{2}; 4π][/m] принадлежат корни:

[m]x= \frac{3π}{4}+2π=\frac{11π}{4}[/m]

[m] x =3π; x=4π[/m]

( см. рис.)