Задача 58215 ...
Условие
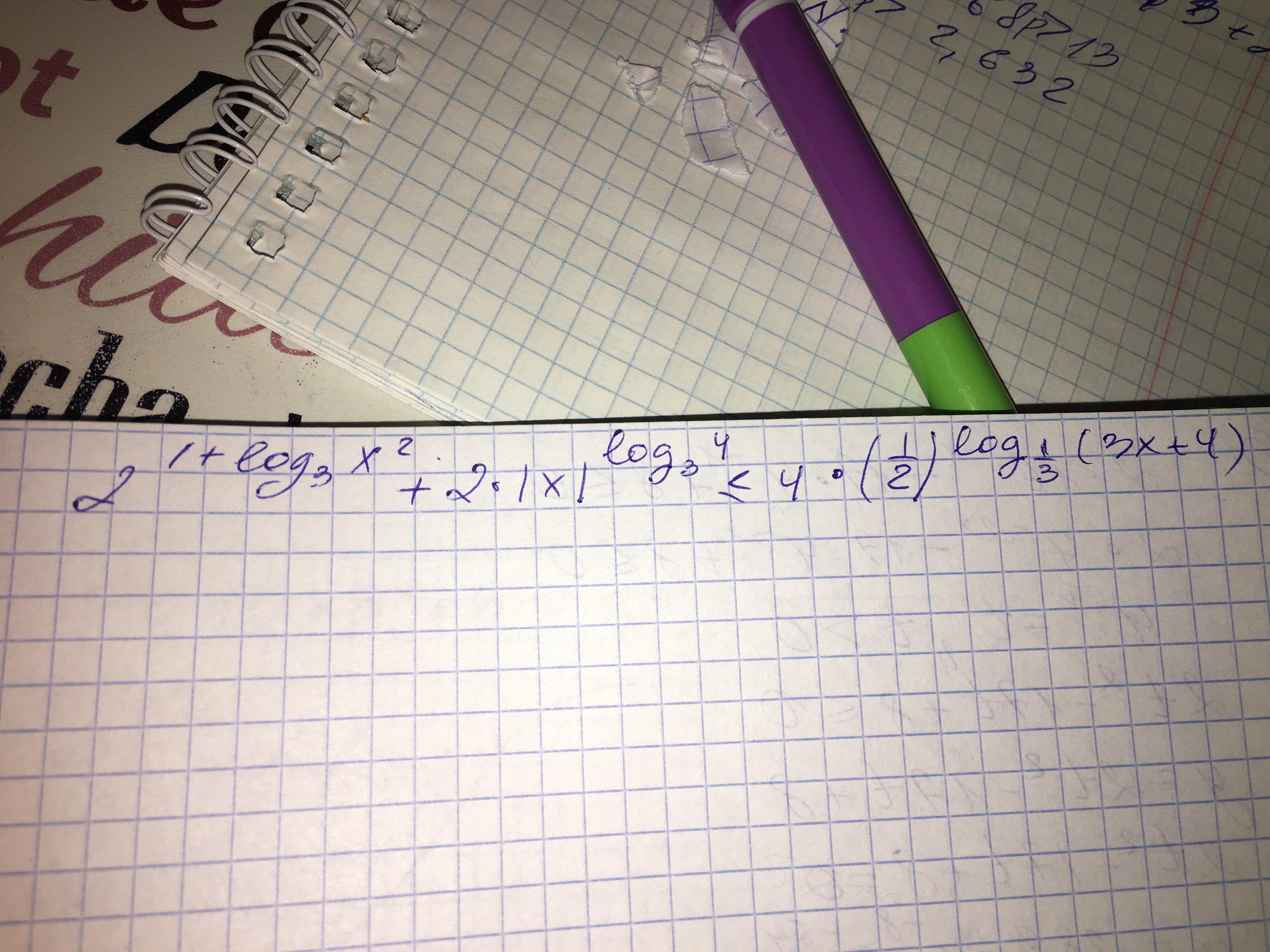
математика 10-11 класс
1399
Решение
★
С помощью этого тождества легко доказать, что
[m] |x|^{log_{3}4}=4^{log_{3}|x|}=(2^{2})^{log_{3}|x|}=(2)^{2log_{3}|x|}=2^{log_{3}|x|^2}=2^{log_{3}x^2}[/m]
Поэтому неравенство принимает вид:
[m]2\cdot 2^{log_{3}x^2}+2\cdot 2^{log_{3}x^2} ≤ 4\cdot (2^{-1})^{log_{\frac{1}{3}}(3x+4)}[/m]
Упрощаем:
[m]4\cdot 2^{log_{3}x^2} ≤ 4\cdot (2^{-1})^{log_{3^{-1}}(3x+4)}[/m]
[m] 2^{log_{3}x^2} ≤ 2^{log_{3}(3x+4)}[/m]
Теперь нет проблем, ОДЗ не забудьте...