Задача 58143 ...
Условие
(log₅(x + 3) - log₅(x - 3))² - 7(log₅(x + 3) - log₅(x - 3)) - 4a² - 6a + 10 = 0
имеет ровно два корня.
Решение
[m]log_{5}(x+3)-log_{5}(x-3)=t[/m]
Получаем квадратное уравнение:
[m]t^2-7t-4a^2-6a+10=0[/m]
D=(-7)^2-4*(-4a^2-6a+10)=9+16a^2+24a=(4a+3)^2
[m]t_{1}=\frac{7-4a-3}{2}[/m] или [m]t_{2}=\frac{7+4a+3}{2}[/m]
Обратный переход:
[m]log_{5}(x+3)-log_{5}(x-3)=\frac{7-4a-3}{2}[/m] или [m]log_{5}(x+3)-log_{5}(x-3)=\frac{7+4a+3}{2}[/m]
[m]log_{5}\frac{x+3}{x-3}=2-2a[/m] или [m]log_{5}\frac{x+3}{x-3}=5+2a[/m]
Каждое из этих уравнений должно иметь корни.
Корень и первого и второго уравнения должен удовлетворять ОДЗ данного уравнения:
[m]\left\{\begin {matrix}x+3>0\\x-3>0\end {matrix}\right.[/m] ⇒[red][m] x > 3[/m][/red]
Решаем первое уравнение:
[m]log_{5}\frac{x+3}{x-3}=2-2a[/m] ⇒ [m] 5^{2-2a}=\frac{x+3}{x-3}[/m]
Переформулируем вопрос.
При каких значениях параметра а уравнение имеет корень, удовлетворяющий неравенству [red] x > 3[/red]
Решаем второе уравнение:
[m]log_{5}\frac{x+3}{x-3}=5+2a[/m] ⇒ [m] 5^{5+2a}=\frac{x+3}{x-3}[/m]
Переформулируем вопрос.
При каких значениях параметра а уравнение имеет корень, удовлетворяющий неравенству [red] x > 3[/red]
Осталось решить две задачи с параметром.
Рассуждаю, что даст графическое решение каждого из уравнений.
График функции
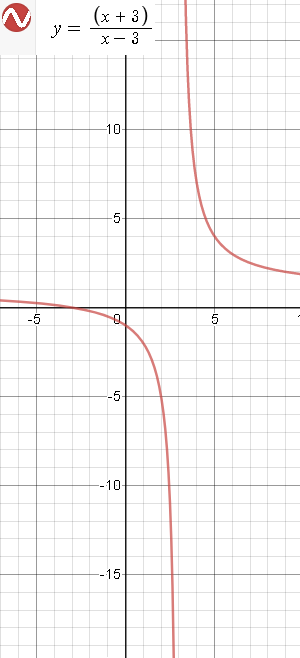
[m]y=\frac{x+3}{x-3}[/m] - гипербола ( см. рис.)
[m]y=1+\frac{6}{x-3}[/m]
Прямая y=1 - [i]горизонтальная асимптота [/i]
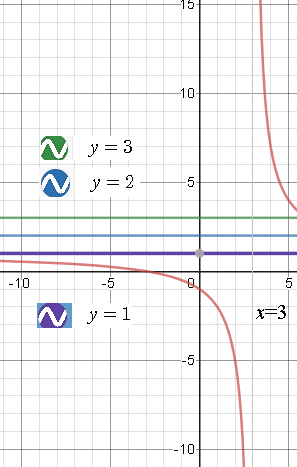
Графики
[m] y=5^{2-2a}[/m] и [m] y=5^{5+2a}[/m] - прямые, параллельные оси Ох
Они должны пересекать гиперболу в одной точке, причем так, чтобы абсцисса точки пересечения была правее 3,
а ордината больше 1
[m] 5^{2-2a}>1[/m] ⇒ [m]2-2a >0[/m]
и
[m] 5^{5+2a}>1[/m] ⇒ [m]5+2a >0[/m]
Два решения:
(-2,5;1)