Задача 58138 Провести полное исследование указанных...

maybe

27 февраля 2021 г. в 01:34

Провести полное исследование указанных функций и построить их графики.

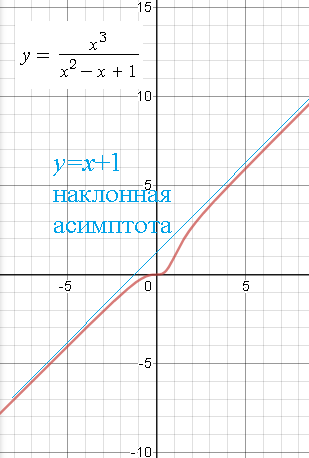
2.10. y = x³/(x² – x + 1)

5f3ea7e3faf909182968ddd9

27 февраля 2021 г. в 08:05

★

Область определения (– ∞ ;+ ∞ )

так как x²–x+1 > 0

D=1–4 <0

Поэтому вертикальных асимптот нет

Горизонтальных асимптот нет, так как

lim_{x →+ ∞} x³/(x²–x+1)= +∞
lim_{x →– ∞} x³/(x²–x+1)= –∞

Наклонная асимптота y=x+1

так как

k= lim_{x → ∞} f(x)/x=lim_{x → ∞} x³/x·(x²–x+1)=1

b= lim_{x → ∞} (f(x)–kx)= lim_{x → ∞} (x³/(x²–x+1)–x)=

= lim_{x → ∞} (x³–x²+x²–x)/(x²–x+1)=lim_{x → ∞} (x²–x)/(²–x+1)=1



y`=((x<sup>3</sup>)`·(x²–x+1)–x³·(x²–x+1)`)/(x²–x+1)²=

=(3x²·(x²–x+1)–x³·(2x–1))/(x²–x+1)²=

=(3x⁴–3x³+3x²–2x⁴+x³)/(x²–x+1)=

=(x⁴–2x³+3x²)/(x²–x+1)=

=x²·(x²–2x+3)/(x²–x+1)


y`=0

x²·(x²–2x+3)=0

x²=0 или x²–2x+3=0 – корней нет D<0

x=0


y` ≥ 0 при любых х из ОДЗ

Функция возрастает на ОДЗ